基本介紹
- 中文名:同餘類
- 外文名:congruence class或residue class
- 領域:數學
同餘符號



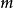




同餘類







餘數系統




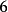



性質
整除性
換句話說,

傳遞性

保持基本運算


除法原理
同餘關係式
威爾遜定理

費馬小定理





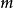















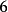









要注意的是,對於同一個模數n,不同的同餘類不等價,亦即,屬於不同同餘類的整數不同餘於模數n,或者說,模n餘數系統中的任二元素不同餘於模n;而且,整數域中的...
剩餘類,亦稱同餘類,是一種數學的用語,為數論的基本概念之一。設模為n,則根據餘數可將所有的整數分為n類,把所有與整數a模n同餘的整數構成的集合叫做模n的一個...
上的同餘關係,等價類 _ 又稱為同餘類。在同餘關係的定義中,式( 蘊含 )還可以改為:對S中的任意元素a,b,c,蘊含 且同餘關係同態與同餘關係 編輯 同餘...
設A和B是兩個代數結構,f是A到B的態射,則A等價關係Φ:a~b若且唯若f(a)=f(b)是A上的一個同餘類,並且A/Φ同構於f的像(B的子代數)。...
如果一個模m的同餘類Kr中任一數與m互質,則稱Kr是與模m互質的剩餘類;在與模m互質的每個剩餘類中任取一個數(共f(m)個)所組成的數組,稱為模m的一個簡化...
縮同餘類的概念在近世代數中有套用,若A是模m的縮同餘類,把滿足Ax=C1的惟一的縮同餘類x表示成A-1,則Ax=B的惟一解可記為x=BA-1=A-1B(或寫成B/A),即...
在同餘理論中,模 n 的互質同餘類組成一個乘法群,稱為整數模 n 乘法群,也稱為模 n 既約剩餘類。在環理論中,一個抽象代數的分支,也稱這個群為整數模 n 的...
的重要公式。Euler函式的定義:模 的同餘類 稱為是模 的既約 (或互素)同餘類,如果 。模 的所有既約同餘類的個數記作 ,通常稱為Euler函式。 [3] 定理...
1 同餘2 同餘類與剩餘系3(M)的性質與Fermat-Euler定理4 Wlison 定理第四章 同餘方程1 同餘方程的基本概念2 一次同餘方程3 一次同餘方程組,孫子定理...
是BCI代數,A,B是X的任意兩理想,若對任意的二,yE (AUB)均有ArnBy}s},則稱x為正則BCI代數,其中As , B,分別表示在X中關於理想A,B的x與y的同餘類.每一...
