基本介紹
定義,證明,舉例,Euler函式的計算公式,
定義
設 是一個非空的含有有限多個元素的集合,
是一個非空的含有有限多個元素的集合, 為一個正整數,
為一個正整數,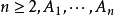 是
是 的
的 個子集。若以
個子集。若以 表示
表示 中具有性質
中具有性質 的元素全體構成的集合,則可知:在
的元素全體構成的集合,則可知:在 中既不具有性質
中既不具有性質 ,又不具有性質
,又不具有性質 ,...,又不具有性質
,...,又不具有性質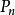 的元素的個數為
的元素的個數為


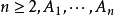








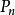
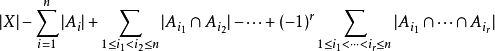
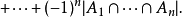
證明
我們用 表示任一個有限集合
表示任一個有限集合 中元素的個數。若
中元素的個數。若 為空集,則令
為空集,則令 。
。




設 是一個非空的含有有限多個元素的集合,
是一個非空的含有有限多個元素的集合, 為一個正整數,
為一個正整數,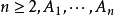 是
是 的
的 個子集,則可以證明
個子集,則可以證明


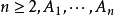








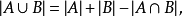
若用 表示
表示 的任一子集
的任一子集 在
在 中的余集(即
中的余集(即 是由
是由 中的不在
中的不在 中的元素構成的),則有
中的元素構成的),則有














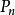
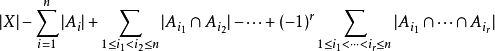
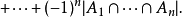
舉例
例如,若 表示正整數,
表示正整數,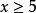 ,集合
,集合 定義為
定義為

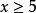





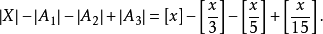
Euler函式的計算公式
套用逐步淘汰原則,就很容易得到計算歐拉函式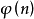 的重要公式。
的重要公式。
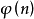
Euler函式的定義:模 的同餘類
的同餘類 稱為是模
稱為是模 的既約 (或互素)同餘類,如果
的既約 (或互素)同餘類,如果 。模
。模 的所有既約同餘類的個數記作
的所有既約同餘類的個數記作 ,通常稱為Euler函式。
,通常稱為Euler函式。






定理 若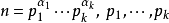 是不同的素數,則
是不同的素數,則