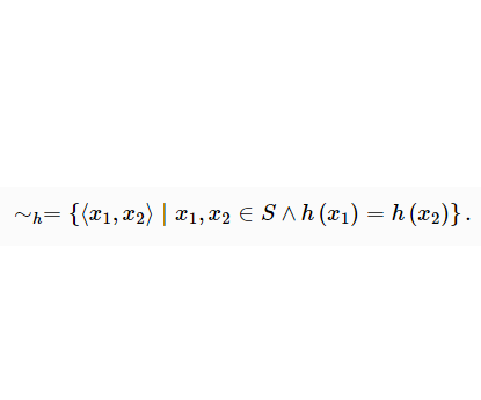同餘關係是代數系統的集合中的等價關係,並且在運算的作用下,能夠保持關係的等價類。以二元運算為例,在a1*a2中,如果用集合S中與a1等價的任何其他元素b1代換a1,並且用與a2等價的任何其他元素b2代換a2,則所求的結果b1*b2與a1*a2位於同一等價類之中。此外,同餘關係與運算密切相關。如果一個代數結構中有多個運算,則需要考察等價關係對於所有這些運算是否都有代換性質。如果等價關係在一個運算上不滿足代換性質,該等價關係就不是代數系統上的同餘關係。
基本介紹
- 中文名:同餘關係
- 外文名:cougruence relation
- 所屬學科:數學
- 相關概念:商代數,同態等
同餘關係的意義,同態與同餘關係,性質,定理1,同餘關係的套用,定義,定理2,定理3,定理4,
同餘關係的意義
設~為代數結構 的載體S上的等價關係,稱~為s上關於一元運算△的同餘關係(congruence relation),如果對S中的任何元素a,b,
的載體S上的等價關係,稱~為s上關於一元運算△的同餘關係(congruence relation),如果對S中的任何元素a,b,



稱~為S上的關於二元運算* 的同餘關係,如果對S中的任何元素a,b,c,d,


當~關於 中一元運算△、二元運算* 均為同餘關係時,便稱~為
中一元運算△、二元運算* 均為同餘關係時,便稱~為 上的同餘關係,等價類
上的同餘關係,等價類 _ 又稱為同餘類。
_ 又稱為同餘類。



在同餘關係的定義中,式( 蘊含
蘊含 )還可以改為:對S中的任意元素a,b,c,
)還可以改為:對S中的任意元素a,b,c,





同態與同餘關係
性質
如果函式 是
是 到
到 的同態映射,那么h導出的S上如下定義的關係
的同態映射,那么h導出的S上如下定義的關係 ,必定是
,必定是 上的同餘關係:
上的同餘關係:






定理1
設h是 到
到 的同態映射,那么等價關係
的同態映射,那么等價關係 是代數結構
是代數結構 上的同餘關係。
上的同餘關係。




同餘關係的套用
定義
設S上的等價關係~為 上的同餘關係,定義S/~上的一元運算@和二元運算
上的同餘關係,定義S/~上的一元運算@和二元運算 如下,對任意
如下,對任意 ,
,



@




定理2
設<S/~,@, >為
>為 的關於~的商代數,那么
的關於~的商代數,那么


在代數結構 與其商代數<S/~,@,
與其商代數<S/~,@, >之間,存在一個有趣的同態映射,稱為規範映射,定義如下:
>之間,存在一個有趣的同態映射,稱為規範映射,定義如下:



定理3
設~為 上的同餘關係,那么規範映射
上的同餘關係,那么規範映射 為
為 到其商代數<S/~,@,
到其商代數<S/~,@, >的一個同態。
>的一個同態。