基本介紹
- 中文名:線性運算
- 外文名:linear operation
- 特點:加法和數量乘法
- 舉例:矩陣的線性運算、向量的線性運算
矩陣的線性運算
矩陣加減法

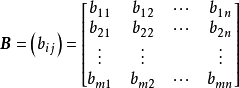
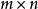
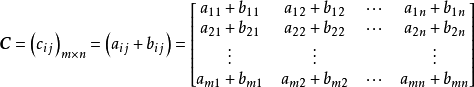
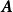
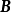
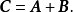
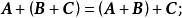

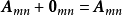

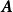
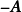
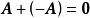
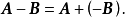
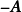
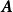
矩陣數量乘積
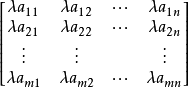
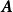
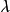

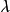
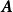
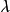
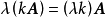
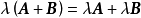
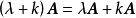
向量的線性運算
向量的加減法
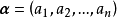
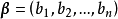
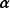
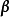
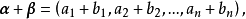
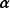
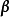
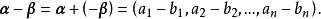
向量的數乘
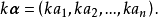
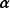
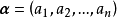
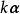
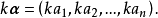
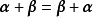
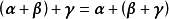
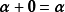
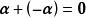

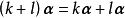
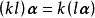
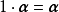
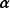
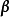

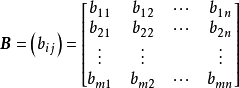
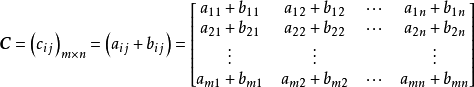
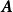
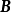
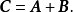
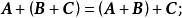

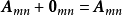

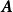
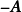
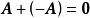
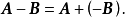
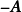
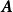
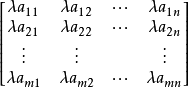
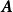
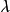

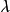
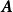
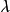
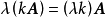
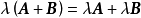
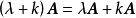
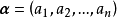
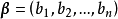
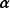
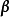
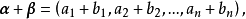
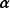
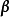
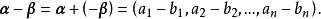
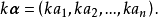
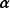
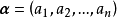
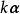
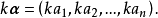
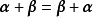
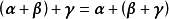
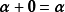
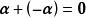

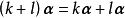
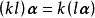
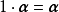
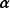
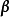
線性運算是加法和數量乘法, 在實數領域像只包含加法和數量乘法二元一次方程就屬於線性運算,如y=3x+5。如果是矩陣的加法和數乘運算,就稱為矩陣的線性運算;如果是...
線性特性是卷積運算的性質之一,即設a,b為任意常數,則對於函式f(z,y),h(x,y)和g(x,y),{af(x,Y)+bh(z,y)}*g(z,y)=-af(x,y)*g(x,y)+bh...
線性規劃計算,責任者是潘平奇著,出版者是科學出版社。...... 線性規劃計算,責任者是潘平奇著,出版者是科學出版社。書名 線性規劃計算 作者 潘平奇 ISBN 978-...
線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身的線性...
線性特性是卷積運算的性質之一,即設a,b為任意常數,則對於函式f(z,y),h(x,y)和g(x,y),{af(x,Y)+bh(z,y)}*g(z,y)=-af(x,y)*g(x,y)+bh...
線性系統是一數學模型,是指用線性運算子組成的系統。相較於非線性系統,線性系統的特性比較簡單。線性系統需滿足線性的特性,若線性系統還滿足非時變性(即系統的輸入...
線性回歸方程是利用數理統計中的回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法之一。線性回歸也是回歸分析中第一種經過嚴格研究並在實際...
線性代數的重要概念之一.設σ是數域P上的線性空間V的一個變換.若對於V中的任意向量α,β與P中的任意數k,有σ(α+β)=σ(α)+σ(β),σ(kα)=kσ(...
卷積是一種線性運算,圖像處理中常見的mask運算都是卷積,廣泛套用於圖像濾波。castlman的書對卷積講得很詳細。高斯變換就是用高斯函式對圖像進行卷積。高斯運算元可以...
