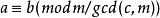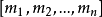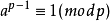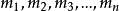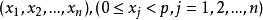基本介紹
- 中文名:同餘定理
- 外文名:Congruence theorem
- 屬性:數學概念
- 記法:a≡b(mod d)
- 性質:反身性、對稱性、傳遞性等
- 相關定理:歐拉定理、費馬小定理、孫子定理
理論背景,同餘符號,定義,證明,性質,相關定理,
理論背景
數學上,兩個整數除以同一個整數,若得相同餘數,則二整數同餘(英文:Modular arithmetic,德文:Kongruenz)。同餘理論常被用於數論中。最先引用同餘的概念與符號者為德國數學家高斯。同餘理論是初等數論的重要組成部分,是研究整數問題的重要工具之一,利用同餘來論證某些整除性的問題是很簡便的。同餘是數學競賽的重要組成部分。
公元972年,在一份阿拉伯手稿中,提出了這樣一個問題:一個正整數n何時能成為一個一個由三個有理平方數形成的等差數列的公差,也就是說x-n,x,x+n都是平方數。十三世紀,義大利數學家斐波那契指出5和7是同餘數,他也猜想1、2、3不是同餘數,但未能給出證明。直到1659年,法國大數學家費爾馬運用他自己發明的無窮下降法證明了1、2、3不是同餘數。十八世紀,大數學家歐拉首次證明了7是同餘數。1952年,Heegner證明了任意模8餘5、7的素數和任意模4餘3的素數的兩倍均為同餘數。2000年,美國克雷數學研究所公布了千禧年七大數學難題,每破解其中一個難題者將獲得100萬美元的獎金。其中就有著名的BSD猜想(全稱Birch and Swinnerton-Dyer猜想),而這個猜想與同餘數問題有緊密的聯繫。2012年,田野證明了存在無窮多個具有任意指定素因子個數的同餘數,這是在同餘數問題上的一個根本性突破,也首次給出了解決BSD猜想的線索。
同餘符號
兩個整數a、b,若它們除以整數m所得的餘數相等,則稱a與b對於模m同餘或a同餘於b模m。
記作:a≡b (mod m),
讀作:a同餘於b模m,或讀作a與b對模m同餘,例如26≡2(mod 12)。
定義
設m是大於1的正整數,a、b是整數,如果m|(a-b),則稱a與b關於模m同餘,記作a≡b(mod m),讀作a與b對模m同餘。
顯然,有如下事實
(1)若a≡0(mod m),則m|a;
(2)a≡b(mod m)等價於a與b分別用m去除,餘數相同。
證明
充分性:m|(a-b)→a≡b(mod m)。
設a=mq1+r1,b=mq2+r2,
且0≤r1,r2<m,
∵m |(a-b),
又a-b=m(q1-q2)+(r1-r2)。
∴必有常數n使得(r1-r2)=mn。
則有m|(r1-r2)。
∵0≤r1,r2<m,
∴0≤|r1-r2|<m,
∴r1-r2=0,
即r1=r2,故a≡b(mod m)。
必要性:a≡b(mod m)→m|(a-b)。
設a,b用m去除餘數為r,
即a=mq1+r,b=mq2+r。
∵m(q1-q2)=(a-b),
∴m|(a-b)。
性質
1.反身性:a≡a (mod m);
2.對稱性:若a≡b(mod m),則b≡a (mod m);
3.傳遞性:若a≡b(mod m),b≡c(mod m),則a≡c(mod m);
4.同餘式相加:若a≡b(mod m),c≡d(mod m),則a c≡b
c≡b d(mod m);
d(mod m);


5.同餘式相乘:若a≡b(mod m),c≡d(mod m),則ac≡bd(mod m)。
證明:
∵a≡b(mod m)∴m|(a-b) 同理m|(b-c),
∴m|[(a-b)+(b-c)]∴m|(a-c).
故a≡c(mod m).
6.線性運算:如果a ≡ b (mod m),c ≡ d (mod m),那么
(1)a ± c ≡ b ± d (mod m);
(2)a * c ≡ b * d (mod m)。
證明:
(1)∵a≡b(mod m),
∴m|(a-b)
同理 m|(c-d)
∴m|[(a-b)±(c-d)]
∴m|[(a±c)-(b±d)]
∴a ± c ≡ b ± d (mod m)
(2)∵ac-bd=ac-bc+bc-bd=c(a-b)+b(c-d)
又 m|(a-b) , m|(c-d)
∴m|(ac-bd)
∴a * c ≡ b * d (mod m)
特殊地, 則
則 ;
;


9.若 ,n=m,則
,n=m,則 ;
;


相關定理
1.歐拉定理:設a,m∈N,(a,m)=1,則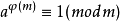 ,
,
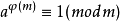
(註:φ(m)指模m的簡系個數, φ(m)=m-1,如果m是素數;

3.中國剩餘定理(孫子定理):


令x為從1到n,ajxj的和,則x適合下列聯立同餘式,

另:求自然數a的個位數字,就是求a與哪一個一位數對於模10同餘。
一次同餘式和孫子定理同餘式的求解中,一次同餘式是最基本的。設整係數n次(n>0)多項式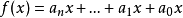 ,(1)m是一個正整數且不能整除αn,則
,(1)m是一個正整數且不能整除αn,則 叫做模m的n次同餘式。如果整數α是(1)的解且
叫做模m的n次同餘式。如果整數α是(1)的解且 ,那么α也是(1)的解,因此(1)的不同解是指滿足(1)的模 m互不同餘的數。對於一次同餘式
,那么α也是(1)的解,因此(1)的不同解是指滿足(1)的模 m互不同餘的數。對於一次同餘式 有解的充分必要條件是(α,m)│b),若有解則有(α,m)個解。一次同餘式組是指
有解的充分必要條件是(α,m)│b),若有解則有(α,m)個解。一次同餘式組是指 。 (2)
。 (2)
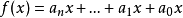







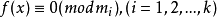

素數為模的同餘式關於素數為模的同餘式,1770年,J.-L.拉格朗日證明了如下定理:設p是素數,那么模 p的n次同餘式的解數不大於 n(重解也計算在內)。人們稱之為拉格朗日定理。由此立即可以得威爾森定理:如果 p是素數,那么(p-1)!+1≡0(mod p)。因為x-1≡0(mod p)有p-1個解1,…,p-1,故由拉格朗日定理可得
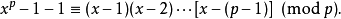
將x=0代入上式得-1≡(-1)(p-1)!(mod p),這就證明了威爾森定理。威爾森定理的逆定理也是成立的,可用反證法簡單證出。用拉格朗日定理還可證明:當p≥5是一個素數時,則有同餘。這個定理是1862年,由J.沃斯頓霍姆證明的。
早在1801年,C.F.高斯就研究了同餘式 的解的個數,這裡
的解的個數,這裡 和同餘式
和同餘式 的解的個數,這裡
的解的個數,這裡 。
。




設ƒ(x)模 p無重因式,1924年,E.阿廷猜想同餘式 ,在ƒ(x)的次數為3和4時,N分別滿,1936年,H.哈塞證明了這一猜想,並且還證明了對於一般含q個元的有限域,把以上兩式中p換成q,也是對的。1948年,韋伊對於一般的ƒ(x,y)=0在有限域上得到類似的結果,他猜想對於
,在ƒ(x)的次數為3和4時,N分別滿,1936年,H.哈塞證明了這一猜想,並且還證明了對於一般含q個元的有限域,把以上兩式中p換成q,也是對的。1948年,韋伊對於一般的ƒ(x,y)=0在有限域上得到類似的結果,他猜想對於 也有類似的結果。1973年,P.德利涅證明了韋伊猜想。他的傑出工作獲得了1978年的國際數學家會議的費爾茲獎。
也有類似的結果。1973年,P.德利涅證明了韋伊猜想。他的傑出工作獲得了1978年的國際數學家會議的費爾茲獎。