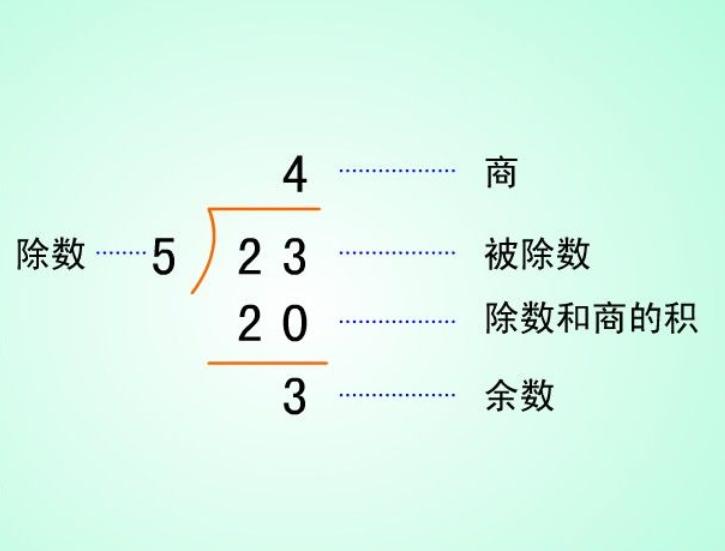
基本解釋
餘數指
整數除法中被除數未被除盡部分,且餘數的取值範圍為0到除數之間(不包括除數)的整數。例如:27除以6,
商數為4,餘數為3。
一個數除以另一個數,要是比另一個數小的話,商為0,餘數就是它自己。例如:1除以2,商數為0,餘數為1;2除以3,商數為0,餘數為2。
定義
在整數的除法中,只有能整除與不能整除兩種情況。當不能整除時,就產生餘數,所以餘數問題在國小數學中非常重要。
取餘數運算:
a mod b = c 表示 整數a除以整數b所得餘數為c。
餘數的計算公式:c = a -⌊ a/b⌋ * b
其中,⌊ ⌋為向下取整運算符,向下取整運算稱為Floor,用數學符號⌊ ⌋表示
例:⌊ 3.476 ⌋=3,⌊6.7546⌋=6,⌊-3.14159⌋= -4
如 7 mod 3 = 7-⌊7/3⌋*3=7-2*3=1
性質
餘數有如下一些重要性質(a,b,c均為自然數):
(1)餘數和除數的差的絕對值要小於除數的絕對值(適用於實數域);
(2)被除數=除數×商+餘數;
除數=(被除數-餘數)÷商;
餘數=被除數-除數×商。
(3)如果a,b除以c的餘數相同,那么a與b的差能被c整除。例如,17與11除以3的餘數都是2,所以17-11能被3整除。
(4)a與b的和除以c的餘數(a、b兩數除以c在沒有餘數的情況下除外),等於a,b分別除以c的餘數之和(或這個和除以c的餘數)。例如,23,16除以5的餘數分別是3和1,所以(23+16)除以5的餘數等於3+1=4。注意:當餘數之和大於除數時,所求餘數等於餘數之和再除以c的餘數。例如,23,19除以5的餘數分別是3和4,所以(23+19)除以5的餘數等於(3+4)除以5的餘數。
(5)a與b的乘積除以c的餘數,等於a,b分別除以c的餘數之積(或這個積除以c的餘數)。例如,23,16除以5的餘數分別是3和1,所以(23×16)除以5的餘數等於3×1=3。注意:當餘數之積大於除數時,所求餘數等於餘數之積再除以c的餘數。例如,23,19除以5的餘數分別是3和4,所以(23×19)除以5的餘數等於(3×4)除以5的餘數。
性質(4)(5)都可以推廣到多個自然數的情形。
例題分析
例1:5120除以一個兩位數得到的餘數是64,求這個兩位數。
分析與解:
5120-64=5056,5056應是除數的整數倍。將5056分解質
因數,得到5056=64×79。
由性質(1)知,除數應大於64,再由除數是兩位數,得到除數在67~99之間,
符合題意的5056的
約數只有79,所以這個兩位數是79。
例2:被除數、除數、商與餘數之和是2143,已知商是33,餘數是52,求被除數和除數。
解:因為被除數=除數×商+餘數=除數×33+52,
被除數=2143-除數-商-餘數=2143-除數-33-52=2058-除數,
所以 除數×33+52=2058-除數,所以 除數=(2058-52)÷34=59,
被除數=2058-59=1999。
答:被除數是1999,除數是59。
例3:甲、乙兩數的和是1088,甲數除以乙數商11餘32,求甲、乙兩數。
解:因為 甲=乙×11+32,
所以 甲+乙=乙×11+32+乙=乙×12+32=1088,
所以 乙=(1088-32)÷12=88,
甲=1088-乙=1000。
答:甲數是1000,乙數是88。
例4:有一個整數,用它去除70,110,160得到的三個餘數之和是50。求這個數。
分析與解:先由題目條件,求出這個數的大致範圍。因為50÷3=16……2,所以三個餘數中至少有一個大於16,推知除數大於16。由三個餘數之和是50知,除數不應大於70,所以除數在17~70之間。
由題意知(70+110+160)-50=290應能被這個數整除。將290
分解質因數,得到290=2×5×29,290在17~70之間的約數有29和58。
因為110÷58=1……52>50,所以58不合題意。所求整數是29。
例5:求478×296×351除以17的餘數。
分析與解:先求出乘積再求餘數,計算量較大。根據性質(5),可先分別計算出各因數除以17的餘數,再求餘數之積除以17的餘數。
478,296,351除以17的餘數分別為2,7和11,(2×7×11)÷17=9……1。所求餘數是1。
例6:甲、乙兩個代表團乘車去參觀,每輛車可乘36人。兩代表團坐滿若干輛車後,甲代表團餘下的11人與乙代表團餘下的成員正好又坐滿一輛車。參觀完,甲代表團的每個成員與乙代表團的每個成員兩兩合拍一張照片留念。如果每個膠捲可拍36張照片,那么拍完最後一張照片後,相機里的膠捲還可拍幾張照片?
分析與解:甲代表團坐滿若干輛車後餘11人,說明甲代表團的人數(簡稱甲數)除以36餘11;兩代表團餘下的人正好坐滿一輛車,說明乙代表團餘36-11=25(人),即乙代表團的人數(簡稱乙數)除以36餘25;甲代表團的每個成員與乙代表團的每個成員兩兩合拍一張照片,共要拍“甲數×乙數”張照片,因為每個膠捲拍36張,所以最後一個膠捲拍的張數,等於“甲數×乙數”除以36的餘數。
因為甲數除以36餘11,乙數除以36餘25,所以“甲數×乙數”除以36的餘數等於11×25除以36的餘數。
(11×25)÷36=7……23,
即最後一個膠捲拍了23張,還可拍36-23=13(張)。
由例6看出,將實際問題轉化為我們熟悉的數學問題,有助於我們思考解題。
例7:5397被一個質數除,所得餘數是15.求這個質數.
解:這個質數能整除
5397-15=5382,
而 5382=2×31997×13×23.
因為除數要比餘數15大,除數又是
質數,所以它只能是23.
當被除數較大時,求餘數的一個簡便方法是從被除數中逐次去掉除數的整數倍,從而得到餘數。
例8:求 645763除以7的餘數。
解:可以先去掉 7的倍數630000餘15763,再去掉14000還餘下 1763,再去掉1400餘下363,再去掉350餘13,最後得出餘數是6.這個過程可簡單地記成
645763→15763→1763→363→13→6.
如果演算能力強,上面過程可以更簡單地寫成:
645763→15000→1000→6.
如果兩個數被同一個除數除餘數相同,那么這兩個數之
差就能被那個除數整除。
例9:有一個大於 1的整數,它除967,1000,2001得到相同的餘數,那么這個整數是多少?
解:由上面的結論,所求整數應能整除 967,1000,2001的兩兩之差,即
1000-967=33=3×11,
2001-1000=1001=7×11×13,
2001-967=1034=2×11×47.
請注意,我們不必求出三個差,只要求出其中兩個就夠了。因為另一個差總可以由這兩個差得到。
例如,求出差1000-967與2001-1000,
那么差
2001-967=(2001-1000)+(1000-967)
=1001+33
=1034
甲、乙兩數,如果被同一除數來除,得到兩個餘數,那么甲、乙兩數之和被這個除數除,它的餘數就是兩個餘數之和被這個除數除所得的餘數。
例如,57被13除餘5,152被13除餘9,那么57+152=209被13除,餘數是5+9=14被 13除的餘數1.
例10:有一串數排成一行,其中第一個數是15,第二個數是40,從第三個數起,每個數恰好是前面兩個數的和,問這串數中,第1998個數被3除的餘數是多少?
解:我們可以按照題目的條件把這串數寫出來,再看每一個數被3除的餘數有什麼規律,但這樣做太麻煩。根據上面說到的結論,可以採取下面的做法,從第三個數起,把前兩個數被3除所得的餘數相加,然後除以3,就得到這個數被3除的餘數,這樣就很容易算出前十個數被3除的餘數,列表如下:
從表中可以看出,第九、第十兩數被3除的餘數與第一、第二兩個數被3除的餘數相同。因此這一串數被3除的餘數,每八個循環一次,因為
1998= 8×249+ 6,
所以,第1998個數被3除的餘數,應與第六個數被3除的餘數一樣,也就是2.
一些有規律的數,常常會循環地出現.我們的
計算方法,就是循環制.計算鐘點是
1,2,3,4,5,6,7,8,9,10,11,12
這十二個數構成一個循環。
按照七天一輪計算天數是
日,一,二,三,四,五,六.這也是一個循環,相當於一些
連續自然數被7除的餘數
0, 1, 2, 3, 4, 5, 6的循環,用循環制計算時間:鐘錶、星期、月、四季,說明人們很早就發現循環現象.用數來反映循環現象也是很自然的事。
循環現象,我們還稱作具有“
周期性”,12個數的循環,就說周期是12,7個數的循環,就說周期是7.例 10中餘數的周期是8。研究數的循環,發現周期性和確定周期,是很有趣的事。
下面我們再舉出兩個餘數出現循環現象的例子。在講述例題之前,再講一個從帶餘
除式得出的結論:
甲、乙兩數被同一除數來除,得到兩個餘數.那么甲、乙兩數的積被這個除數除,它的餘數就是兩個餘數的積,被這個除數除所得的餘數.
例如,37被11除餘4,27被11除餘5,37×27=999被 11除的餘數是 4×5=20被 11 除後的餘數 9。
1997=7×285+2,就知道1997×1997被7除的餘數是2×2=4.
例 11:191997被7除余幾?
解:從上面的結論知道,191997被7除的餘數與21997被7除的餘數相同.我們只要考慮一些2的連乘,被7除的餘數.
先寫出一列數
2,2×2=4,2×2×2 =8,
2×2×2×2=16,…
然後逐個用7去除,列一張表,看看有什麼規律。列表如下:
事實上,只要用前一個數被7除的餘數,乘以2,再被7除,就可以得到後一個數被7除的餘數.(為什麼?請想一想.)
從表中可以看出,第四個數與第一個數的餘數相同,都是2.根據上面對餘數的計算,就知道,第五個數與第二個數餘數相同,……因此,餘數是每隔3個數循環一輪。循環的周期是3。
1997=3×665 +2
就知道21997被7除的餘數,與21997 被 7除的餘數相同,這個餘數是4。
再看一個稍複雜的例子。
例12:70個數排成一行,除了兩頭的兩個數以外,每個數的三倍都恰好等於它兩邊兩個數的和.這一行最左邊的幾個數是這樣的:
0,1,3,8,21,55,…
問:最右邊一個數(第70個數)被6除余幾?
解:首先要注意到,從第三個數起,每一個數都恰好等於前一個數的3倍減去再前一個數:
3=1×3-0,
8=3×3-1,
21=8×3-3,
55=21×3-8,
……
不過,真的要一個一個地算下去,然後逐個被6去除,那就太麻煩了。能否從前面的餘數,算出後面的餘數呢?能!同算出這一行數的辦法一樣(為什麼?),從第三個數起,餘數的計算辦法如下:
將前一個數的餘數乘3,減去再前一個數的餘數,然後被6除,所得餘數即是
用這個辦法,可以逐個算出餘數,列表如下:
注意,在算第八個數的餘數時,要出現0×3-1這在國小數學範圍不允許,因為我們求被6除的餘數,所以我們可以 0×3加6再來減 1
從表中可以看出,第十三、第十四個數的餘數,與第一、第二個數的餘數對應相同,就知道餘數的循環周期是 12
70 =12×5+10
因此,第七十個數被6除的餘數,與第十個數的餘數相同,也就是4。
“今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二,問物幾何?”按照如今的話來說:
一個數除以3餘2,除以5餘3,除以7餘2,求這個數。
這樣的問題,也有人稱為“韓信點兵”.它形成了一類問題,也就是初等數論中解
同餘式.這類問題的有解條件和解的方法被稱為“中國剩餘定理”,這是由中國人提出的。許多國小數學的課外讀物都喜歡講這類問題,但是它的一般解法決不是小學生能弄明白的。這裡,我們通過兩個例題,對較小的數,介紹一種通俗解法。
例13:有一個數,除以3餘2,除以4餘1,問這個數除以12餘幾?
解:除以3餘2 的數有:
2, 5, 8, 11,14, 17, 20, 23…
它們除以12的餘數是:
2,5,8,11,2,5,8,11,…
除以4餘1的數有:
1, 5, 9, 13, 17, 21, 25, 29,…
它們除以12的餘數是:
1, 5, 9, 1, 5, 9,…
一個數除以12的餘數是唯一的.上面兩行餘數中,只有5是共同的,因此這個數除以12的餘數是5
上面解法中,我們逐個列出被3除餘2的整數,又逐個列出被4除餘1的整數,然後逐個考慮被12除的餘數,找出兩者共同的餘數,就是被12除的餘數.這樣的列舉的辦法,在考慮的數不大時,是很有用的,也是同學們最容易接受的。
如果我們把例23的問題改變一下,不求被12除的餘數,而是求這個數.很明顯,滿足條件的數是很多的,它是
5+ 12×整數
整數可以取0,1,2,…,無窮無盡.事實上,我們首先找出5後,注意到12是3與4的
最低公倍數,再加上 12的整數倍,就都是滿足條件的數.這樣就是把“除以3餘2,除以4餘1”兩個條件合併成“除以12餘5”一個條件。《孫子算經》提出的問題有三個條件,我們可以先把兩個條件合併成一個.然後再與第三個條件合併,就可找到答案.
例14:一個數除以 3餘2,除以5餘3,除以7餘2,求符合條件的最小數.
解:先列出除以 3餘2的數:
2, 5, 8, 11, 14, 17, 20, 23, 26,…,
再列出除以5餘3的數:
3, 8, 13, 18, 23, 28,….
這兩列數中,首先出現的公共數是8.3與5的最低公倍數是15.兩個條件合併成一個就是
8+15×整數,
列出這一串數是
8, 23, 38,…,
再列出除以7餘2的數
2, 9, 16, 23, 30,…,
就得出符合題目條件的最小數是23.
事實上,我們已把題目中三個條件合併成一個:被105除餘23.
最後再看一個例子.
例15:在100 至200之間,有三個連續的自然數,其中最小的能被3整除,中間的能被5整除,最大的能被7整除,寫出這樣的三個連續自然數.
解:先找出兩個連續自然數,第一個能被3整除,第二個能被5整除(又是被3除餘1).例如,找出9和10,下一個連續的自然數是11.
3和5的最低公倍數是15,考慮11加15的整數倍,使加得的數能被7整除.11+15×3=56能被7整除,那么54,55,56這三個連續自然數,依次分別能被3,5,7整除.
為了滿足“在100至200之間”將54,55,56分別加上3,5,7的最低公倍數105.所求三數是
159, 160, 161。