帶餘除法就是帶有餘數的除法,被除數=除數×商+餘數。帶餘除法主要包括整數的帶餘除法和多項式的帶餘除法。其中,整數的帶餘除法定理為:對於任意的a,b(設a≥b且b≠0),存在唯一的商q和餘數r 使得a=bq+r。多項式的帶餘除法則與之類似。
基本介紹
- 中文名:帶餘除法
- 外文名: division algorithm
- 學科:數學
- 用於:數論
- 類屬:定理
- 包括:整數帶餘除法和多項式帶餘除法
定理
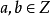

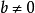
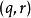
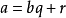
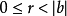
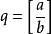
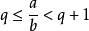


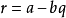

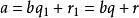



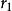
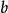
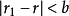
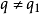
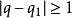
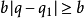
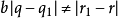
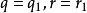
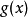
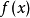
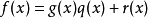


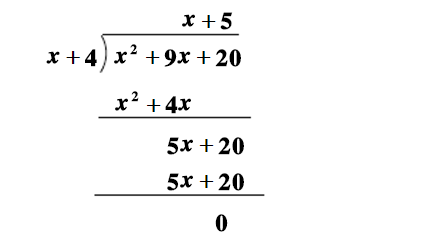
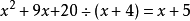
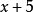

套用
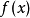
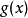

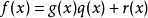
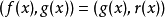
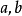

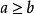
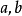
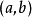

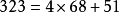
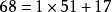



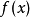
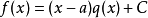
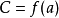
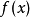
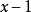
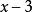
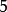
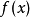
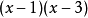
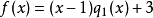

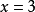

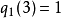
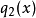

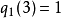
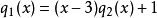

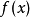
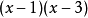
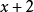
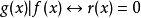
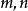
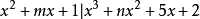
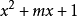
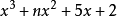

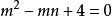
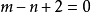
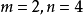
帶餘除法就是帶有餘數的除法,被除數=除數×商+餘數。帶餘除法主要包括整數的帶餘除法和多項式的帶餘除法。其中,整數的帶餘除法定理為:對於任意的a,b(設a≥b且b≠0),存在唯一的商q和餘數r 使得a=bq+r。多項式的帶餘除法則與之類似。
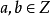

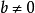
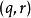
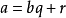
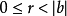
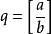
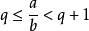


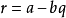

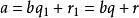



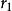
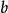
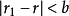
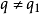
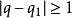
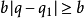
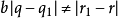
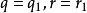
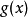
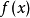
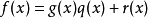


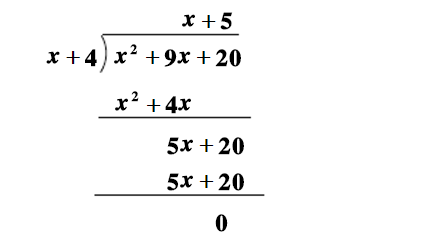
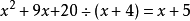
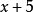

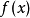
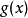

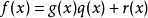
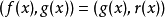
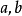

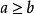
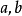
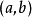

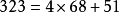
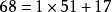



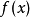
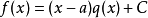
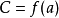
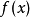
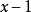
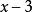
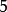
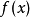
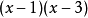
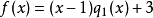

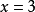

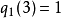
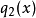

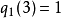
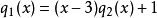

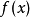
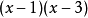
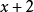
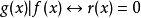
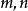
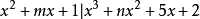
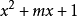
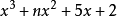

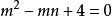
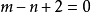
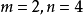
帶餘除法就是帶有餘數的除法,被除數=除數×商+餘數。帶餘除法主要包括整數的帶餘除法和多項式的帶餘除法。其中,整數的帶餘除法定理為:對於任意的a,b(設a≥b...
帶餘數除法也稱為除數算法。...... 圖集 帶餘數除法圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:5次歷史版本 最近更新: 創建者:陌上花開流年...
餘數指整數除法中被除數未被除盡部分,且餘數的取值範圍為0到除數之間(不包括除數)的整數。[1] 例如:27除以6,商數為4,餘數為3。...
多項式帶餘除法 若f(x)和g(x)是F[x]中的兩個多項式,且g(x)不等於0,則在F[x]中有唯一的多項式 q(x)和r(x),滿足ƒ(x)=q(x)g(x)+r(x),...
歐氏環(Euclid ring)是比主理想整環更窄的環類。它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R°=R\{0}到非負整數集內的一...
。所以若用乘法的逆來定義除法,這個除法不能成為一個二元運算(即不符合封閉性,即使不允許除以0)。但我們可以用帶餘除法作為替代。 現設a,b為自然數, ,則有自...
帶餘除法(一)帶餘除法(二)有趣的被除數餘數的妙用除數是10的除法二年級上冊練習指導練一練四第7題練一練十一第8題練一練十七第4題“除數是10的除法”練與...
1.1 整除的概念與帶餘除法 11.1.1 整除及其性質 11.1.2 素數 41.1.3 帶餘除法 51.2 整數的表示 71.3 最大公因數與輾轉相除法 8...
輾轉相除法是求最大公因式的一種行之有效的方法,過程敘述如下:設 、 是數域 上的多項式且不全為0,不妨設 。利用帶餘除法,以 除 得 。若 ,再以 除 得...
1.4 帶餘除法與同餘 第二章 有理數 2.1 有理數的計算技巧 2.2 絕對值 2.3 填數問題 第三章 一元一次方程(組) 3.1 一元一次方程 3.2 一次方程組 第...
斯圖姆定理(Sturm theorem)是確定實係數多項式實根個數的一個重要定理,設f(x)是實係數n(n≥1)次多項式,令f0(x)=f(x),f1(x)=f′(x),則由帶餘除法,...
{ return a=a*b; } //除法和取模先實現一個帶餘除法函式 Wint divmod(Wint &a,const Wint &b) { Wint ans; for(int t=a.size()-b.size(); a>...
《初等數論難題集(第1卷)》全書共分10章:第1章整除與帶餘除法,第2章因子與倍數,第3章最大公約數與最低公倍數,第4章平方數與n次方數,第5章素數與合數,...
1.2.1 帶餘除法 4 1.2.2 最大公因數 5 1.2.3 歐幾里德算法 7 1.3 最低公倍數 13 1.4 算術基本定理 15 習題1 16 第2章 同餘 18 2.1 同餘的...
本書包括正文7章及附錄:自然數的基本性質,整除性、素數及算術基本定理,帶餘除法、最大公因數及最低公倍數,輾轉相除法與線性丟番圖方程,同餘式、剩餘類及中國...
2.帶餘除法.對於形如}2<x>/[P(二)]‘的既約分式,其中P(二)為不可約多項式,Q(二)一a, (x)P‘一’(x)+az(x)1'‘一z(x)++ak一, (x)P(x)...
2. 多項式整除、帶餘除法、最大公因式、輾轉相除法 3. 互素、不可約多項式、重因式與重根. 4. 多項式函式、餘數定理、多項式的根及性質. 5.代數基本定理、復...
