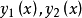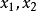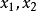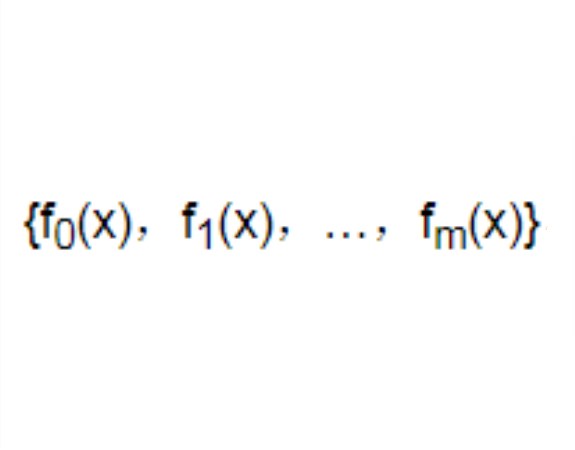斯圖姆定理(Sturm theorem)是確定實係數多項式實根個數的一個重要定理，設f(x)是實係數n(n≥1)次多項式，令f0(x)=f(x)，f1(x)=f′(x)，則由帶餘除法，f0(x)=f1(x)q1(x)+r1(x).令f2(x)=-r1(x)，對f1(x)與f2(x)，由帶餘除法有f1(x)=f2(x)q2(x)+r2(x)，再令f3(x)=-r2(x)，並對f2(x)與f3(x)作帶餘除法，如此繼續下去，得多項式序列：f0(x)，f1(x)，…，fs(x)，…，fm(x)，稱為f(x)的斯圖姆序列，斯圖姆定理是：設f(x)是實係數多項式，且f(x)無重根，f0(x)，f1(x)，…，fm(x)是f(x)的斯圖姆序列，若a<b，f(a)≠0和f(b)≠0，則序列f0(a)，f1(a)，…，fm(a)的變號數V(a)與序列f0(b)，f1(b)，…，fm(b)的變號數V(b)的差V(a)-V(b)恰是f(x)在區間(a，b)內實根的個數，斯圖姆(C.-F.Sturm)在1829年的論文《論數字方程解》中，深入地討論了代數方程根的隔離，引入了斯圖姆序列的概念，給出了斯圖姆定理。
基本介紹
- 中文名：斯圖姆定理
- 外文名：Sturm theorem
- 所屬學科：數學
- 所屬問題：高等代數(多項式)
- 發現者：斯圖姆(J.C.F.Sturm, 1803-1855)
基本介紹,相關說明,
基本介紹
斯圖姆定理是判斷實係數多項式方程實根個數的定理。給出實係數多項式方程
f(x)=a0xn+…+an-1x+an=0， a0≠0，
令f0(x)=f(x)，f1(x)=f′(x)，用f1(x)除f0(x)得商q1(x)及餘式-f2(x)，一般地有
fk-1(x)=fk(x)qk(x)－fk+1(x)，(k=1，2，…，m)，
直到fm+1(x)≡0為止，得到m+1個多項式序列
{f0(x)，f1(x)，…，fm(x)}，
稱為以f0及f1為基的斯圖姆序列，當x=a時，
{f0(a)，f1(a)，…，fm(a)}
是一個數列。若其中兩個相鄰數符號相反就稱為一次變號，記此數列變號次數為Va，若f(a)≠0，f(b)≠0，且數列
{f0(b)，f1(b)，…，fm(b)}
的變號次數為Vb，則f(x)=0在[a，b]內共有Va-Vb個不相同的實根，設最後非零函式fm(x)沒有實根，則f(x)=0的實根都是單根，若fm(x)=0有實根，則這些根都是f(x)=0的重根，其重數為fm(x)=0內的重數加1，這就是斯圖姆定理的內容。當a=-∞，b=+∞時，則得f(x)=0實根個數；當(a，b)內只有一個根且b-a很小，則可解決實根的隔離問題。
相關說明
(1)斯圖姆分離定理是一個關於二階線性微分方程零解的定理：設
為方程y"+q(x)y=0的兩個線性無關的解。若
分別使
為零，則
在之間至少有一個零點。
(2)斯圖姆比較定理是一個重要定理：已知兩個方程y"+q1(x)y=0，z"+q2(x)z=0，且在(a, b)內q2(x)≥q1(x)， 則在第一個方程任一解的兩個零點之間，至少有第二個方程每個解的一個零點。
斯圖姆定理可用於研究滿足齊次邊界條件的方程y"+q(x)y=λy的斯圖姆——柳維爾問題。
1829年，法國數學家斯圖姆得出了求實係數代數方程在已知區間上的實根個數的簡單方法——斯圖姆方法，而這方法的依據就是斯圖姆定理，劉維爾說:“由於這一巨大的發現，斯圖姆立即簡化並且完整了代數的原理，用新的解法充實了它們。”
斯圖姆(J.C.F.Sturm, 1803-1855)是原籍瑞士的法國數學家。
