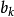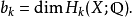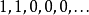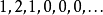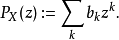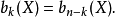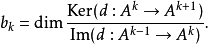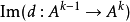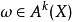相關詞條
- 貝蒂數
在代數拓撲學中,拓撲空間之貝蒂數 是一族重要的不變數,取值為非負整數或無窮大。...... 在代數拓撲學中,拓撲空間之貝蒂數 是一族重要的不變數,取值為非負整數或...
- 貝蒂定理
在代數拓撲學中,拓撲空間之貝蒂數 b0,b1,b2,… 是一族重要的不變數,取值為非負整數或無窮大。直觀地看,b0 是連通成份之個數,b1 是沿著閉曲線剪開空間而保持...
- 貝蒂,E.
貝蒂,E.義大利數學家。1823年10月21日生於皮斯托亞,1892年8月11日卒於比薩。在比薩大學學習數學,曾參加義大利獨立戰爭,後在皮斯托亞中學教數學。1865年獲比薩大學...
- 貝蒂(美國卡通品牌)
貝蒂(Betty Boop),美國卡通品牌,誕生於1930年代,是由美國紐約Fleischer兄弟工作室設計製造的卡通(動畫)人物。Betty初期被創作為一隻備有人身體的狗貝蒂扮演當時片中...
- 貝蒂·伯伊德
貝蒂·伯伊德(Pattie Boyd),曾用名貝蒂·伯伊德·哈里森或貝蒂·克萊普頓,(1944年3月17日-)是一位英國模特兒和攝影師。她因先後嫁給兩位搖滾音樂家喬治·哈里森和...
- 貝蒂·弗里丹
貝蒂·弗里丹(Betty Friedan,1921-2006),美國當代著名的女權運動家和社會改革家,自由主義女性主義思想代表人物之一。貝蒂·弗里丹作為20世紀美國女性主義代表人物之一,...
- 貝蒂寄生蟲
貝蒂寄生蟲,學名:cerathotoa italica,也被網友稱為“外星寄生蟲”,主要以魚類的舌頭為食,吸食魚類舌頭血液生長。2012年3月媒體報導稱貝蒂寄生蟲在地中海被發現,...
- 貝蒂(貝蒂寄生蟲)
貝蒂是科學家在地中海最新發現一種類似外星生物的可怕寄生蟲,能夠逐漸吞食笛鯛科等魚類的舌頭,然後代替魚類的“舌頭”在其口腔中等待進一步的傳播。...
- 貝蒂一布里奇曼狀態方程
貝蒂一布里奇曼狀態方程(Beattie-Bridgeman equation of state), 是描述實際氣體系統處於平衡狀態時摩爾體積,壓力p,及溫度T之間關係的一種經驗方程,具有高度準確性。...
- 貝蒂·卡爾曼
貝蒂·卡爾曼:瑜伽教練。現居住在澳大利亞的墨爾本,雖年過古稀,但身手矯健,可輕鬆完成許多高難度瑜伽動作,包括用雙手支撐身體,並保持平衡的“孔雀式”,身體往後仰...
- 小貝蒂(漫畫)
《小貝蒂》是王曉明自1985年在《幽默大師》雜誌上連載迄今已二十多年,是該刊唯一不間斷、連載時間最長的欄目,影響了數代人,成為該刊最受歡迎、讀者來信最多的...
- 貝蒂(1823-1892)
貝蒂(1823-1892)Enrico Betti ,義大利數學家。...... 1871 年引進的“貝蒂數”,是重要的拓撲不變數。在黎曼影響下,研究數學物理,證明貝蒂定理(彈性論互逆定理),...
- 恩里科·貝蒂
恩里科·貝蒂(Enrico Betti,1823年10月21日——1892年8月11日),義大利數學家,1823年10月21日生於皮斯托亞,1892年8月11日卒於比薩。...
- 貝蒂E
貝蒂是義大利數學家,英文名稱Enrico Betti (1823~1892) .1823年10月21日生於皮斯托亞,1892 年8月11日卒於比薩。薩大學學習數學,曾參加意利獨立戰爭,後在...
- 代數拓撲
單純復形的n-階同調群的自由階等於n-階貝蒂數(Betti number),所以可以直接使用單純復形的同調群來計算它的歐拉特徵數。作為另外一個例子,閉流形的最高維的積分...
- 愛與數學
第5章 辮群與貝蒂數 053第6章 敲開數學世界的大門 067第7章 把一個個小島連線起來 085第8章 神奇的猜想 097第9章 現代數學的“羅塞塔石碑” 119...
- 黑色大麗花慘案
1947年1月15日,美國加利福尼亞,洛杉磯,中心住宅區39街,諾頓街區。上午10點左右,一名叫貝蒂·勃辛格的家庭主婦帶著自己3歲的女兒去鞋匠那裡取送修的鞋子,當她們...