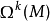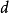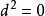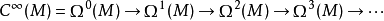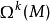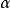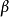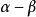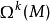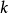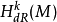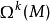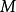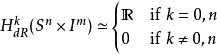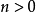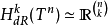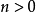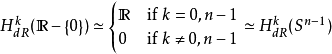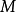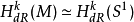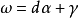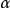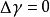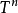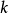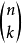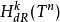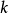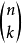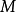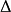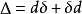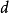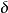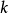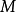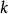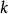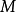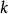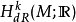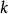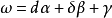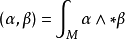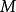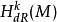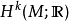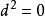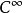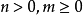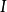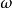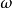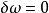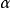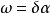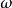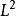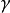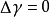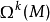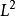德拉姆上同調

德拉姆上同調(de Rham cohomology) 是同時屬於代數拓撲和微分拓撲的工具。它能夠以一種特別適合計算和用具體的上同調類的方式表達關於光滑流形的基本拓撲信息。它是基於有特定屬性的微分形式的存在性的上同調理論。它以不同的確定的意義對偶於奇異同調，以及Alexander- Spanier 上同調。

基本介紹

• 中文名：德拉姆上同調
• 外文名：de Rham cohomology
• 用處：代數拓撲和微分拓撲的工具
• 證明時間：1931年

基本介紹

定義

任何光滑流形上的光滑微分-形式在加法之下形成一個交換群(實際上也是一個實向量空間，稱為

外導數給了以下的映射

下面是一個基本的關係

;

這本質上是因為二階導數的對稱性。所以-形式和外導數形成一個上鏈復形(cochain complex),稱為de Rham復形:

微分幾何術語中，是其它微分形式的外導數的形式稱為恰當形式(exact form)，而外導數為0的形式稱為閉形式；這個關係說明

恰當的微分形式都是閉的

其逆命題卻一般來說不成立；閉形式未必恰當。de Rham上同調的想法就是給一個流形上不同類型的閉形式分類。分類這樣進行，如果中的兩個閉形式和是上同調的，如果他們相差一個恰當形式，也就是，若為恰當形式。這個分類導出一個中的閉形式空間的一個等價關係。然後定義階 de Rham上同調群為

等價類的集合，也就是，中閉形式模恰當形式。

注意，對所有有n個連通分量的流形，

這是因為M上導數為零的函式在每個連通分量上為常數。

例證

例1

通常我們可以通過已知的0上同調羣和Mayer-Vietoris序列來計算一個流形的其他的德拉姆上同調羣。另一個有用的事實是德拉姆上同調是同倫不變數。下面是一些常見拓撲對象的上同調羣，但我們沒有給出計算步驟：

n-球:

對於n-球，或者球和一個開區間的乘積，我們有以下結果。令, 而為一個實開區間. 則:

n-圓環:

類似的， 令，可以得到：

穿孔歐幾里得空間:

穿孔歐幾里得空間就是拿掉原點的歐幾里得空間。對於， 我們有:

莫比烏斯帶(Möbius strip)，：

大致來說，下面的結果或多或少是因為莫比烏斯帶可"收縮(contract)"為一個1-球（圓）：

調和形式

若是一個緊黎曼流形，則每個中的等價類包含恰好一個調和形式。也就是說，給定閉形式的等價類的任一代表可以寫為

其中是一個形式，而是調和的：。

注意一個緊黎曼流形上的調和函式是一個常數。這樣，這個特殊的代表元素可以視為流形上所有上同調等價的形式中的一個極值(極小值)。例如，在2-圓環上，一個常1-形式可以視為在一個形式，它所有的"毛"都整齊的梳到一個方向(而且所有的毛都一樣長)。這個情況下，這表示2維環的第一貝蒂數是2。更一般的，在一個維環上，可以考慮-形式的各種不同的梳理。有種不同的梳理用來建立的一個基；因此-環的第貝蒂數就是。

更精確的講，對於一個微分流形，可以裝備一個附加的黎曼度量。這樣拉普拉斯運算元可以定義為

其中是外導數，而是余微分。拉普拉斯運算元是齊次的(在分次中)線性微分運算元作用在微分形式的外代數上：我們可以分別來看它在每個階分量上的作用。

若為緊且可定向，拉普拉斯運算元在-形式的空間上的核的維度和階德拉姆上同調群的維度相同(根據霍奇理論:拉普拉斯運算元從閉形式的每個上同調類中挑出唯一的一個調和形式。特別的，所有上的調和-形式同構於。每個這種空間的維度都有限，並有階貝蒂數給出。

Hodge 分解

令為余微分(codifferential)，我們稱形式是上閉的(co-closed)如果而稱其為上確切(co-exact)。若對於某個形式；有。Hodge分解表明任意-形式可以分裂為3個分量:

其中為調和的：。這是因為確切和上確切形式互相正交；他們的正交補就是同時確切和上確切的形式：也就是，調和形式。這裡，正交性由上的內積定義:

精確的定義和分解的證明需要用索伯列夫空間來表述問題。主要的思想就是索伯列夫空間提供了平方可積性和微分形式的柯西列收斂到極限形式的自然設定。這個語言使得我們得以克服緊支撐這樣的限制，就像在Alexander-Spanier上同調中那樣。

de Rham 定理

De Rham定理, 由Georges de Rham在1931年證明，它表明對於一個緊緻可定向光滑流形，群同構於具有奇異上同調群

的實向量空間。楔積賦予這些群的直和一個環結構。定理的進一步結果是這兩個上同調換(作為分次環)是同構的。

一般化的斯托克斯定理是德拉姆上同調和鏈的同調群的對偶性的表達。