積分周期理論

積分周期理論是流形上分析的一個分支，主要研究微分形式的積分周期，這反映了流形的同調特徵。

基本介紹

• 中文名：積分周期理論
• 外文名：integral period theory
• 適用範圍：數理科學

簡介

積分周期理論是流形上分析的一個分支，主要研究微分形式的積分周期，這反映了流形的同調特徵。

1930年，德拉姆(de Rham,G.-W.)引進微分流形M的德拉姆上同調群，並指出它是一個微分不變數與拓撲不變數。還證明了當M為緊緻流形時，M的p維德拉姆上同調群的維數是有限的，等於第p個貝蒂數，這是流形M的微分結構與拓撲結構的一個重要關係。

中心定理

積分周期理論的中心定理是德拉姆定理，它斷言微分流形M的p維德拉姆上同調群與M的p維可微奇異上同調群是同構的。

同構的單性表明所有周期為零的閉微分形式是正合形式，而同構的滿性意味著對每個閉鏈類z賦予一個實數per(z)，則存在一個閉形式α，使對所有的閉鏈z有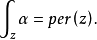

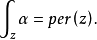
改進

霍奇(Hodge,W.V.D.)對德拉姆理論做了重要改進，他引進調和微分形式，霍奇理論斷言每個德拉姆上同調類存在唯一的調和微分形式。