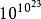龐加萊引理(Poincare Lemma)論述單位球上微分形式的零調性質。因由龐加萊首先提出，所以被命名為龐加萊引理。
基本介紹
- 中文名：龐加萊引理
- 外文名：Poincare's theorem
- 提出者：J.-H.龐加萊
- 提出時間：十九世紀90年代
- 套用學科：熱力學
背景,定義,龐加萊猜想,相關,
背景
1872年玻耳茲曼在研究實際熱力學過程的不可逆性即熱力學第二定律的微觀本質時，曾根據非平衡態的分布函式f（r，v，t）定義了一個函式H，並證明在孤立系統以非平衡態趨於平衡態的過程中，H隨時間單調下降，在平衡態達到最小值，這就是H定理。玻耳茲曼認為，H函式與熵對應，H的減少與熵的增大對應 ，H定理為熱力學第二定律提供了統計解釋。
但是龐加萊定理似乎與H定理相矛盾。根據龐加萊定理，當H函式隨時間單調地減少之後，只要經過足夠長的時間，總可以重新增大，回復到初始的數值。對此，玻耳茲曼的回答是，H定理具有統計性質，即非平衡態總是以絕對優勢的機率趨於平衡態，逆過程並非完全不可能，只是機率極其微小。
定義
龐加萊引理(Poincare Lemma)論述單位球上微分形式的零調性質。該引理斷言:若U是歐氏空間Rn中開單位球體，r(U)是U上微分k形式的空間，則對每個k，1，存在一個線性變換
這個引理有兩個推論:
1。若。是R”中開單位球體上的一個k形式，且dm=0，則存在一個((k一1)形式月使得d月一、
2。 R”中開單位球的德拉姆上同調群對於p)l都為零。
龐加萊猜想
1904年，龐加萊在一篇論文中提出了一個看似很簡單的拓撲學的猜想：在一個三維空間中，假如每一條封閉的曲線都能收縮到一點，那么這個空間一定是一個三維的圓球。但1905年發現其中的錯誤，修改為：“任何與n維球面同倫的n維封閉流形必定同胚於n維球面。”後來這個猜想被推廣至三維以上空間，被稱為“高維龐加萊猜想”。
大於等於五維的龐加萊猜想被史蒂芬·斯梅爾證明；
四維的龐加萊猜想被麥可·弗里德曼證明；
三維的龐加萊猜想被俄羅斯數學家佩雷爾曼於2002-2003年證明。
他們分別獲得1966年，1986年和2006年菲爾茲獎。
相關
論述力學體系運動可復性的定理。1872年L。玻耳茲曼在他的《氣體理論》一文中證明了一個重要的定理──H定理。H定理斷定：一個處於非平衡態的系統總是要單調地趨向平衡；而一個已經達到平衡的系統再自動地趨向非平衡是不可能的。那么，自然會提出這樣的問題:平衡系統自動趨向非平衡是否完全不可能？如果不是完全不可能的，其可能性有多大？1896年E。策爾梅洛就根據J。-H。龐加萊定理研究了運動的可復性問題。
1890年龐加萊證明了下述定理:系統的Γ相空間（見相宇）中除了一個測度為零的點集以外，在t=0時使系統從相空間中任何一有界點P出發，則對於任意給定的一個小距離ε>0，都存在一個有限的時間t(ε)，在這時間間隔內，系統必經過相空間的一點P‵，而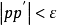
。
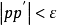
由此定理可以看出運動的可復性。因為從中可以得到結論：放在封閉容器內的任何一個力學體系經過足夠長的時間後，總要回復到任意接近初始狀態的那個狀態上。由此可見，當H函式隨時間單調地減少以後，只要經過足夠長的時間，它將回復到初始的數值。這個結論似乎同巨觀不可逆性相牴觸，同玻耳茲曼H定理相矛盾。
玻耳茲曼對上述矛盾作了明確的回答:H定理具有統計的性質，它只是說非平衡態總以絕對優勢的幾率趨向平衡態，沒有完全否定由平衡態趨向非平衡態的可能性，並不完全排斥H的值偶然增加，運動回復到原狀，只是幾率極其微小，因此反映統計規律的巨觀不可逆性同微觀可逆性並不矛盾。龐加萊定理雖然說明力學系統經過充分長的時間後總可以回復到初始狀態附近，但是，根據龐加萊的證明，對於一般的氣體或液體，若單位體積含有的粒子數為1023的數量級，那么回復時間的數量級約為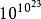
秒，它比迄今知道的宇宙壽命還要大很多的數量級，比趨向平衡的時間大得簡直不可估量，它對所有巨觀物體來說，實際上可以看作是無窮大。於是得出結論：從熵小的狀態走向熵大的狀態幾乎是必然的；而從熵大的狀態走向熵小的狀態幾乎是不可能的。玻耳茲曼 H定理和龐加萊定理可以相容。
