CW復形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的空間。
基本介紹
- 中文名:CW復形
- 外文名:CW complex
- 定義:一類拓撲空間
- 特例:單純復形
- 定義:由胞腔從低維到高維堆積成的空間
簡介
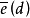
CW復形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的空間。
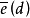
CW復形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的空間。...... CW復形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的...
所有CW復形是吉洪諾夫空間。 所有正規正則空間是完全正則的,而所有正規豪斯多夫空間是吉洪諾夫空間。 Niemytzki平面是吉洪諾夫空間但非正規空間的一個例子。 [1] 吉洪...
有限單純復形或CW復形的貝蒂數有限。當 k 大於復形維度時, 。對於有限 CW 復形,定義其龐加萊多項式為貝蒂數的生成函式對於任意 X,Y,有對於n-維可定向閉流...
代數拓撲學家一般使用緊生成空間、CW復形或譜。 [1] 參考資料 1. Goerss, P. G.; Jardine, J. F., Simplicial Homotopy Theory, Progress in Mathematics ...
數學裡,單純集合(simplical set)是範疇同倫論中一個構造,這是“良態”拓撲空間的一個純代數模型。歷史上,這個模型源自組合拓撲學特別是單純復形。...
胞腔逼近定理(cellular approximation theorem)是代數拓撲學的一條重要定理。與單純逼近類似,CW復形之間的連續映射可以用胞腔映射來逼近。...
2.2 r映射2.3 單純復形與CW復形2.4 收縮核與映射的可擴張性2.5 收縮核的某些繼承性質2.6 形變收縮核與鄰域收縮核第3章 絕對擴張子與絕對鄰域擴張子...
;有時也會考慮較小一類的空間,例如緊生成豪斯多夫空間或CW復形。 [1] 兩空間在同倫範疇中同構的充要條件是它們同倫等價。設X,Y為拓撲空間,它們在同倫範疇中...
47 CW復形的上同調48 上積49 曲面的上同調環第六章 帶任意係數的同調50 張量積51 帶任意係數的同調第七章 同調代數52 Ext函子53 上同調的萬有係數定理...
本書作者以微分流形為中心寫了這本書,涉及拓撲學的廣泛的領域並在分析數學、...9.6 CW復形和進一步的計算參考文獻第10章 上同調10.1 引言10.2 Pontrjagin...
是單連通CW復形、且所有有理同調群都是有限維,則 擁有一個極小蘇利文模型 ,滿足 且所有 的維數都有限。這個蘇利文代數稱作 的蘇利文極小模型,且在同構意義上唯...
4 劉應明,CW復形可乘的一個充要條件,數學學報,1978,21(2):171~175。 5 劉應明、劉立榆,附貼空間的度量化,數學學報,1979,22(2):241~244。〔全文發表於...
(F)作為相應纖維叢的定義.由於這個對應關係,在以後的討論中,將把適用於主叢的理論,也套用到相應的纖維叢上去,特別地,對於分類空間Bc , CW復形X,與.f i , ...
懷特海定理(Whitehead theorem)同倫論中一條重要的定理.懷特海定理斷言:若X,Y都是CW復形,則連續映射.f : X->Y是同倫等價若且唯若它是弱同倫等價.該定理...
在數學領域代數拓撲學的同倫論中,懷特黑德定理說,拓撲空間X和Y之間的連續映射f,誘導出所有同倫群之間的同構,則當X和Y是連通,並都有CW復形的同倫型的時候,f是...
若(X;A,B,x0)是空間的三聯組,使得(A,A∩B)是n連通的相對CW復形(n≥1),(B,A∩B)是m連通的相對CW復形,則由包含映射 誘導的映射 對於1≤r≤m+n是...
設.}W‘表示由所有帶有基點的CW復形以及它們之間所有保持基點的胞腔映射的同倫類所組成的範疇,: }.f表示所有的點集和所有保持基點的函式所組成的範疇.韋琪公理...
1、如果底空間B是一個CW復形,則托姆空間T(ξ)是一個(k-1)連通CW復形,而且相應於B的每個n胞腔有一(=(n+k)胞腔;2、如果ξ是B上定向k平面叢,則每個整...
5.4.1 CW復形5.4.2 例子5.4.3 可縮空間與同倫群5.4.4 基本群5.4.5 高維同倫群5.5 定理5.4.1證明5.6 線性意向與球面5.7 Pareto規則與同倫獨裁5.8 無否決...
在代數拓撲和同倫論中,波斯尼科夫塔(Postnikov Tower或稱:波斯尼科夫系統)是關於CW復形在同倫意義下進行分解的一種方法。形象地說,給定一個連通的CW復形 X,X ...
