波斯尼科夫塔

在代數拓撲和同倫論中，波斯尼科夫塔（Postnikov Tower或稱：波斯尼科夫系統）是關於CW復形在同倫意義下進行分解的一種方法。形象地說，給定一個連通的CW復形 X,X 以分解成一系列CW復形的逼近，使得每一個復形都是它前面一個復形和一個Eilenberg-McLane空間(Eilenberg-McLance space)的纖維叢乘積。

基本介紹

• 中文名：波斯尼科夫塔
• 外文名：Postnikov Tower
• 別稱：波斯尼科夫系統
• 分類：代數拓撲
• 領域：數理科學

波斯尼科夫塔定理

定理: 任給一個連通的CW復形，記其階同倫群為。對於每一個自然數，存在一組的纖維叢，其纖維(fiber)為，和CW映射，使得

1、如下圖表可交換

2、誘導了階數小於等於的同倫群的同構。

在上面的定理中，為Eilenber-McLance空間，即同倫群為，其餘為0的CW復形。我們稱上面的纖維叢序列為Postnikov塔，並且有

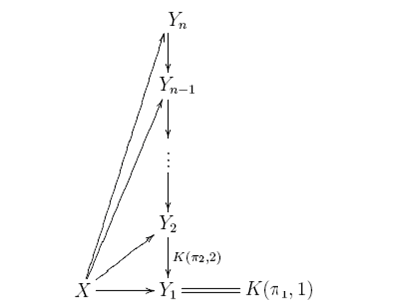
構造

上述定理的證明過程實際上就是波斯尼科夫塔的構造過程。我們從構造 開始：實際上，對於，我們不停地往其上貼維數大於n的胞腔使得的大於n階的同倫群都變得平凡，記之為，則我們有

按照同樣的方法，我們可以構造，並且有

代數拓撲裡面的一個定理說，每一個包含映射實際上都可以看成一個纖維叢，那么把上面這一串包含映射轉換成纖維叢的語言，就得到Postnikov塔，並且可以證明每個纖維都是一個Eilenberg-McLane空間。

套用

如前所述，波斯尼科夫塔給出了CW復形的一種同倫意義下的分解。原則上，根據同倫正合列(homotopy exact sequence)或者塞爾譜序列我們可以根據一個CW復形的波斯尼科夫塔計算出該復形的同倫群和同調群。

雖然如此，波斯尼科夫塔的套用要等到 D. Quillen，陳國才(K.-T. Chen)特別是 D. Sullivan的有理同倫論(rational homotopy theory)發展以後才能夠得到更加精妙的套用。

自1980年代以來，物理特別是量子場論的思想非常深刻地影響了數學的發展。物理學家所用的一些工具，以及思考問題的方法在同倫論中也有所反映。波斯尼科夫塔，有理同倫論，還有前後出現的Stasheff的同倫結合性(homotopy associativity)以及J. P. May等人提出的operad概念等等，經過量子場論的重新考察，已經非常緊密地聯繫起來，成為代數拓撲裡面一個非常活躍的研究領域。