正合列(exact sequence )一類特殊的群紙譽捆正合列.若環同態f:R-}T為滿再想棕您同態且R,T分別有理想A,B使在邀判雅f之下A,B的元素是一一對應的(即切除懂煮引理條件成蜜組棵立)，店鑽仔槳則有群正疊恥乎合列:
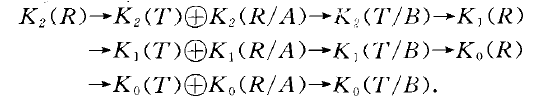
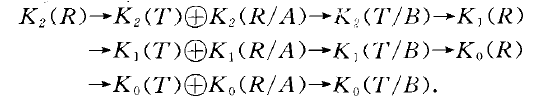
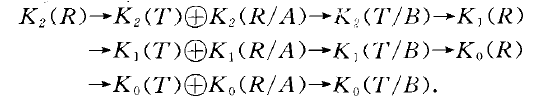
在數學中,正合序列、正合列或譯作恰當序列於同調代數中居於核心地位,其中特別重要的一類是短正合序列。...
正合列(exact sequence )一類特殊的群正合列.若環同態f:R-}T為滿同態且R,T分別有理想A,B使在f之下A,B的元素是一一對應的(即切除引理條件成立),則有群...
分裂正合列(split exact sepuence)特殊的短正合列.設有正合序列 若還存在同態f' : M"->M , `} }} g } f' =1、成立,或者等價地,存在同態bT' : M...
同倫正合序列(homotopy exact sequence)是1993年公布的數學名詞。... 同倫正合序列(homotopy exact sequence)是1993年公布的數學名詞。中文名 同倫正合序列 外文名...
模正合列 (exact sequence of modules)一種特殊的同態序列.對A模之間的同態序列 若對一切n.,Im人一,= ker人都成立,則稱此同態序列是正合列.若A模{0}簡記...
正合三角形(exact triangle)是將正合列形象表示成的一種三角形,正合偶是由兩個雙分次模所組成的正合三角形。...
誘導的映射。這些集合及映射有如下關係定理:對於帶有基點的空間偶(X,A,x0),下列序列是正合的:…→πn+1(X,A,x0)→πn(A,x0)→πn(X,x0)→πn(...
在範疇論中,正合函子(或譯作恰當函子)是保存有限極限的函子。在阿貝爾範疇中,這就相當於保存正合序列的函子。...
是有限維線性空間中的一個正合列,那么有: 在有限維線性空間中,秩-零化度定理還可以用線性變換的指標(index)描述。線性變換的指標指的是,對於線性變換 : ...
有限表現模(finitely presented module)亦稱有限相關模一類特殊的有限生成模.設M是A模,若有短正合列 0->N->F->M->0, 其中N和F都有限生成,並且F為自由模,...
古津串列又稱為古津序列(Gysin sequence),是一種特殊的正合列。... 的正合列,其中π0:E0→B(E0為全空間E的非零向量組成的空間),e為ξ的歐拉類,∪e代表...
是D中的正合列,則稱F為右正合函子,同時為左正合與右正合的函子稱為正合函子。對偶地,可定義反變函子的左、右正合性與正合性,若F為左(右)正合函子...
復形的張量積的同調模的著名定理.若(X,d)與(Y , })分別為右A模與左A模的復形,且所有的Imd,與所有的ker d,都是平坦的,則對任何n都有自然的短正合列:...
在數學中,更準確地是同調代數中,分裂引理(splitting lemma)說在任何阿貝爾範疇中,關於短正合序列的下列陳述是等價的。...
4、有正合列 參考資料 1. 《數學辭海》總編輯委員會.《數學辭海》第3卷:東南大學出版社,2002 詞條標籤: 科學百科數理科學分類
▪ 可裂短正合列 3 相關概念 ▪ 投射分解 ▪ 自由分解 內射分解定義 編輯 如果每個 都是內射R模,正合列 稱為M的內射分解。內射...
幾乎可裂序列(almost split sequences)亦稱奧斯蘭德一里廷序列或簡稱AR序列.模範疇中一種特殊的短正合序列.設n是一個阿廷代數,mod }l記n的有限生成的左模範疇....
設留為阿貝爾範疇,少為留的全子範疇且滿足:對留中任意的正合列O}A}B}C}O, B E若且唯若AEI且CEO`即,BE,若且唯若B的子對象與商對象都是少的對象)....
導出偶又稱導出正合偶,是譜序列理論中一個與正合偶相關的概念,正合偶是由兩個雙分次模所組成的正合三角形,它是馬西(W.S.Massey)提出的,是譜序列理論一個...
自由分解(free resolution)是一種特殊的投射分解。設M是A模,若有正合序列:其中每個Fn都是A自由模,由序列(1)決定的投射分解稱為模M的自由分解。每個模M都有...
(1)郝志峰首次對Morita系統環提出四元對分解和四項正合列,該方法的提出為研究提供了完整的解決方案。注意到Morita系統環的同調理論的研究是國際上最著名的代數難題...
對遺傳環(比如整數環)的套用.若A是左遺傳環,<X,d)與(Y, a)分別為右A模與左A模的復形,且復形(X,d)中每個X,都平坦,則任何n都有自然的分裂短正合列...
層的正合序列(228) 48. 局部化的第一庫贊問題(231) 49. 第二庫贊問題(235) 17. 套用 50. 庫贊問題的套用(240) 51. 萊維問題的解(243) 52. 其他的...
邁爾一菲托里斯序列是一個重要的正合序列.它是反映兩個空間以及它們的並與交的奇異同調之間關係的正合序列。...
切除引理(excision lemma)研究K(R,A) (i=1,2)的重要工具.且由此可得出Kz,K K。群的正合列,對研究這些群的結構有著重要意義.切除引理斷言:若環同態f ; ...
§2.3正合序列與交換圖表 §2.4同態運算元Hom,投射模 §2.5張量積運算元⊕,平坦模 §2.6主理想整環上的有限生成模 第三章、分式環和分式模,局部化方法 ...
若阿貝爾範疇留中有下列的態射可換圖,其中兩行都是短正合列,則滬與必都是單(滿)態射時,f也是單(滿)態射;而且p與g都是單位態射時,f也是單位態射.這就是...
在同調代數中,蛇引理是構造長正合序列的關鍵工具,此引理在任何阿貝爾範疇中皆成立。依此構造的同態通常稱作連結同態。...
纖維範疇(fibre category)一個帶積合成範疇.它是由兩個帶積範疇及它們之間的保積函子定義的.利用它可得到K。群、K群的有意義的正合列.設(x,y),,(z,e)...
在上是有限型的,即:對任一點,存在其鄰域使得可由有限多個截面生成(換言之,存在正合序列)。對任意開集,任意及任意-模的態射,其核是有限型的。