自由分解(free resolution)是一種特殊的投射分解。投射分解是一種特殊的左復形。它是內射分解的對偶概念。設M是A模,M上的零調投射左復形稱為M的投射分解。
基本介紹
- 中文名:自由分解
- 外文名:free resolution
- 領域:數學
- 性質:特殊的投射分解
- 對偶概念:內射分解
- 對象:模
概念
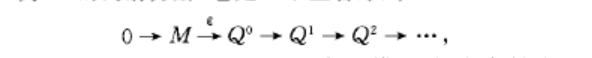
投射分解
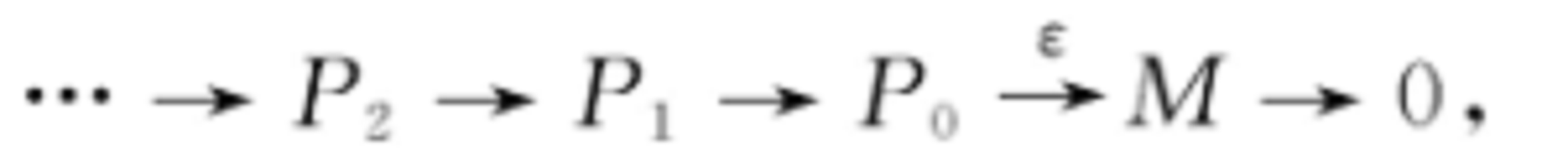
正合序列
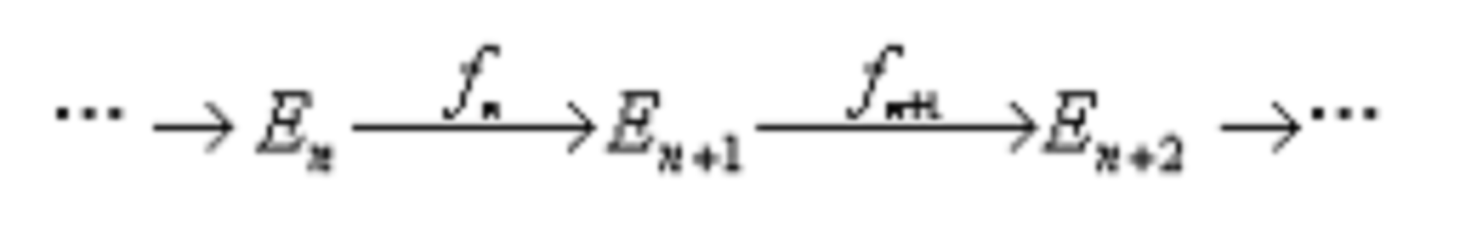
自由分解(free resolution)是一種特殊的投射分解。投射分解是一種特殊的左復形。它是內射分解的對偶概念。設M是A模,M上的零調投射左復形稱為M的投射分解。
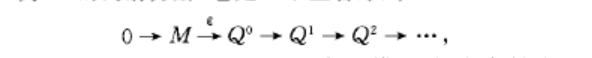
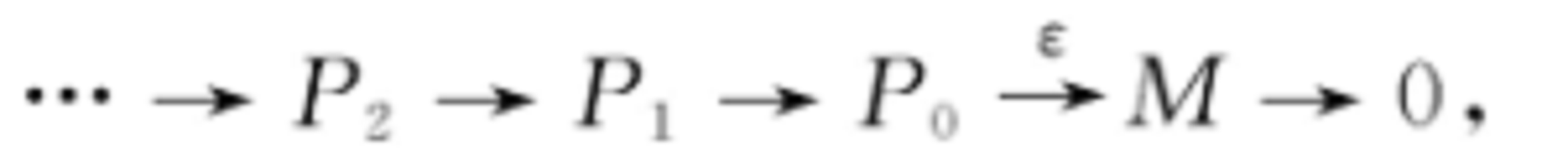
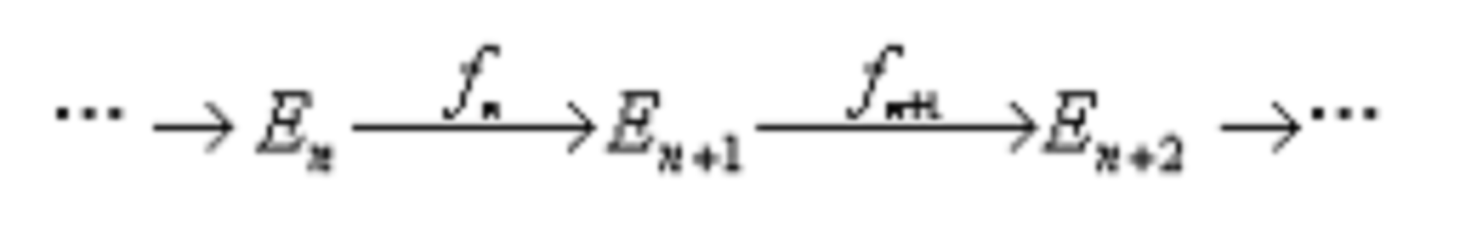
自由分解(free resolution)是一種特殊的投射分解。投射分解是一種特殊的左復形。它是內射分解的對偶概念。設M是A模,M上的零調投射左復形稱為M的投射分解。...
自分解autcdecompnsitinn常溫、常壓下,化合物,如騰(YHs)、腫(.}1sHa )、碘化氮(N13)等發生自分解的反應二如碘化氮受輕震即發生爆炸分解.發生自分解的化台...
斯皮諾達分解的定義,是一類非形核長大型、連續型不穩態相變。固溶體成分位於斯皮諾達(spinodal)線(自由能曲線的拐點連線)之內,其無窮小的成分漲落即引起系統自由能...
投射分解是一種特殊的左復形,它是內射分解的對偶概念。設M是A模,M上的零調投射左復形稱為M的投射分解,它是一個正合序列。...
spinodal分解譯為亞穩分域、調幅分解、隱晶分解、亞穩相分解。在一定合金系統中,固溶體經適當熱處理之後,分解為成分不同的微小區域相間分布的組織。...
拐點分解()。不是通過成核—生長機理而是。在此種方式出溶的早期階段中,在固溶體內並不存在有明顯的兩相界面,且過飽和的組分(例如鉀長石中的Na)在固溶體內的...
分解矩陣(decomposition matrix)群表示論的一個特殊矩陣.即描述與各個不可約常表示相應的模表示的不可約成分重數的矩陣...
曲線自由能成分曲線本質上可以認為這三種相變都是在降溫時從一個單相過飽和固溶體轉變為兩相混合物的分解過程。...
溶劑分解,有時也稱為溶解,為一吸引帶有分子離子溶劑的溶液聚集的過程。當離子在溶劑中溶解,且會被溶劑分子所包圍。...
均裂分解honioiytir dernmpasitinn共價鍵分子a: }.在熱、光等輻射條件下,成為自由基或成為離子。當共價鍵斷裂時,A和Y}各占有1個電子成為A,和B·時稱為均...
自由能源是指利用特殊技術奪取電子電場作為能量輸出,而電子從環境中獲取能量以恢復自身的電場的過程。19世紀80年代末,電子科學的商業期刊預言將要出現“自由能源”。...
內射分解是投射分解的對偶概念。...... 內射分解自由分解 〔free resolution〕自由分解是一種特殊的投射分解。如果每個Pn都是自由R模,正合列 稱為M的自由分解。[1...
自由飛模型(free flight model)是利用飛機的縮比模型在真實大氣中進行的為獲取飛機參數的試驗,從而保證一些飛機高難度動作取得時的飛行安全,是最全面、可靠的試驗...
氧分解是將盛有水的金屬容器同靜電發生器的高壓電極相連線,經過加熱的導電體一端接地,另端靠近水箱水面或置於水面之上。導電體的材質採用碳鋼或鐵合金,水中氫氧...
自由回響是信號與系統學科內的概念。動態電路的完全回響中,已由初始條件確定待定係數k的微分方程通解部分,稱為電路系統的自由回響,它的函式形式是由電路系統本身結構...
由熱引起的無機和有機化合物的分解反應稱之為熱分解。...... 由熱引起的無機和有機化合物的分解反應稱之為熱...反應過程中沒有自由基或離子這一類活性中間體產生...
自由之石(STONE FREE)是《JoJo奇妙冒險》第六部女主角空條徐倫(JOLYNE KUJO)的替身。...
《追尋自由:論經濟倫理自由範疇本義》是2008年吉林大學出版社出版的圖書,作者是羅乾坤。本書基於自由的三個理論傳統:共和主義的傳統、自由派的傳統、唯心主義自由...
《現代自由插花》是2008年化學工業出版社出版的圖書,作者是黎佩霞。...... 《現代自由插花》從插花造型的基本元素和技巧開始,著重介紹如何培養對花材的觀察力,如何...
用作標記的放射性核素放出的射線(見放射性)對標記化合物本身產生的電離輻射分解。...... 標記的放射性核素放出的射線(見放射性)對標記化合物本身產生的電離輻射...
