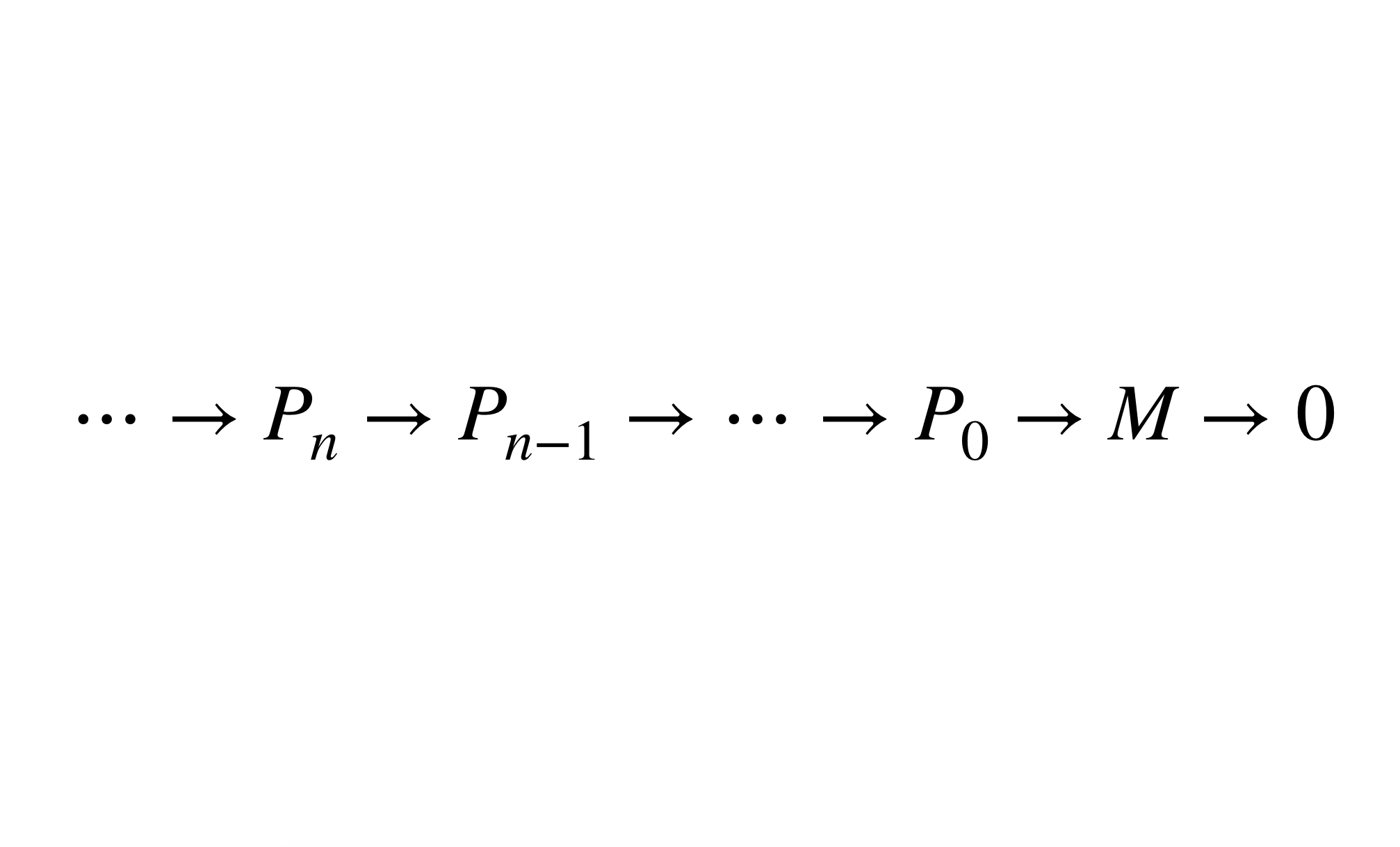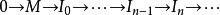投射分解

投射分解是一種特殊的左復形，它是內射分解的對偶概念。設M是A模，M上的零調投射左復形稱為M的投射分解，它是一個正合序列。

基本介紹

• 中文名：投射分解
• 外文名：projective resolution
• 適用範圍：數理科學

定義

設R是環，M是R模，如果每個Pn都是投射R模，正合列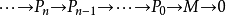稱為M的投射分解。

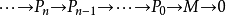
自由分解

〔free resolution〕

自由分解是一種特殊的投射分解。

如果每個Pn都是自由R模，正合列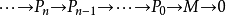稱為M的自由分解。

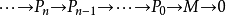
內射分解

〔injective resolution〕

如果每個都是內射R模，正合列稱為M的內射分解。

正合列

〔exact sequence〕

正合列是由交換群和同態組成的序列，並且它在每個交換群處正合，即。

短正合列

〔short exact sequence〕

形如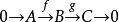的正合列稱為短正合列，此時f是單同態， g是滿同態，且kerg=imf。

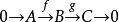
可裂短正合列

〔splitting short exact sequence〕

如果存在同態h:C→B使得，交換群及同態的短正合列稱為可裂短正合列。