基本介紹
- 中文名:投射對象
- 外文名:Projection object
- 領域:數學
簡介
同調代數
阿貝爾範疇
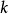
正合函子
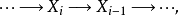
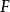
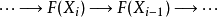
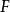
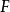
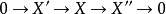
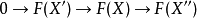
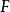
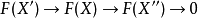
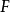
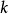
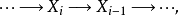
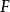
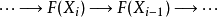
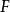
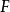
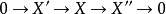
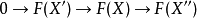
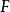
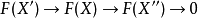
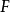
在同調代數中,內射對象與投射對象是內射模與投射模在阿貝爾範疇中的推廣,二者的定義相對偶。...
對象關係映射(Object Relational Mapping,簡稱ORM)是通過使用描述對象和資料庫之間映射的元數據,將面向對象語言程式中的對象自動持久化到關係資料庫中。本質上就是將...
心理學“投射”是一個人將內在生命中的價值觀與情感好惡影射到外在世界的人、事、物上的心理現象。...
投射效應是指將自己的特點歸因到其他人身上的傾向。在認知和對他人形成印象時,以為他人也具備與自己相似的特性的現象,把自己的感情、意志、特性投射到他人身上並強...
投射研究是指套用投射技術的市場調研。 需要運用到的技術有聯想法、圖片回響法、主題類化法等等。...
投射性認同是精神分析的重要概念之一,最早由克萊因提出。在精神分析的客體關係理論里,投射性認同是一個誘導他人以一種限定的方式來作出反應行為模式。它源於一個人...
投射測驗是人格測量方法之一。用於探索個體心理深處的活動。採用一些曖昧的刺激,如墨漬、無結構的圖片等,讓被試在不受限制的條件下作出反應。為減少偽裝,被試通常...
Map,將鍵映射到值的對象。在map中可以使用匿名對象找到一個key對應的value。...... 將鍵映射到值的對象。一個映射不能包含重複的鍵;每個鍵最多只能映射到一個值...
對象自我,也即自我,翻譯自西方心理學中的兩個術語:self ,ego。二者的涵義不同,self指一個獨特、持久的同一身份的我。ego在弗洛伊德精神分析理論中指人格結構的...
通過異形播片系統,我們可以為客戶勾取投影對象——異形物體的輪廓,並根據其輪廓設身打造專用的動態影片,最終通過多通道邊緣融合軟體,使投影完美貼合到異形表面上,...
投影(Projection)運算是指將對象轉換為一種新形式的操作,該形式通常只包含那些將隨後使用的屬性。通過使用投影,您可以構建依據每個對象生成的新類型。...
