基本介紹
定義
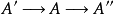
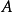
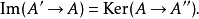
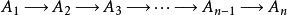
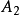
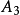
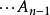
例子
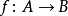
短正合序列
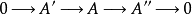
分裂短正合序列
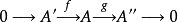
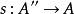
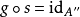
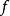
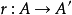
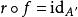
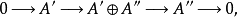
將正合序列拆解為短正合序列
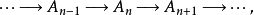
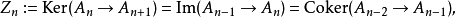
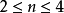
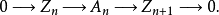
推廣
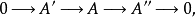
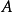
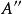
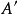
長正合序列
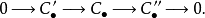
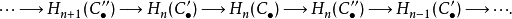
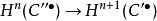
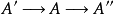
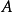
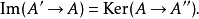
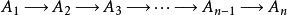
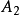
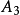
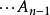
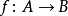
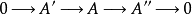
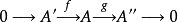
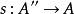
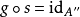
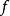
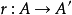
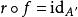
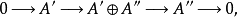
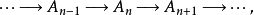
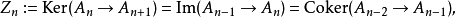
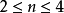
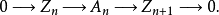
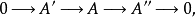
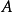
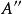
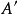
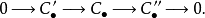
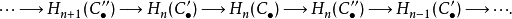
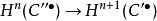
在數學中,正合序列、正合列或譯作恰當序列於同調代數中居於核心地位,其中特別重要的一類是短正合序列。...
正合同倫序列(exact homotopy sequence)是同倫的重要性質之一。是聯繫(絕對)同倫與相對同倫的一種關係。倫型相同的拓撲空間所共有的性質稱為同倫不變數。由於...
在範疇論中,正合函子(或譯作恰當函子)是保存有限極限的函子。在阿貝爾範疇中,這就相當於保存正合序列的函子。...
單純同調序列(simplicial homology sequence)是同調群所具有的一種性質。復形偶(K,L)與K和L的各種同調關係表現為它們的同調群組成的一個正合的序列,即單純同調...
正合三角形(exact triangle)是將正合列形象表示成的一種三角形,正合偶是由兩個雙分次模所組成的正合三角形。...
分裂正合列(split exact sepuence)特殊的短正合列.設有正合序列 若還存在同態f' : M"->M , `} }} g } f' =1、成立,或者等價地,存在同態bT' : M...
最後,若正合序列(M,d)中除三個互相連線的項外皆為0,即即稱為短正合序列。這時 是單射, 是滿射,且 。同調代數的主要內容是研究Hom函子, 函子,及其導出函...
在範疇論中,正合函子(或譯作恰當函子)是保存有限極限的函子。在阿貝爾範疇中,這就相當於保存正合序列的函子。設 為阿貝爾範疇, 為加法函子。若對每個正合...
在抽象代數中,設Q為群,若存在群G,N,及群的正合序列,則稱群G為Q的群擴張,或稱Q對N的擴張。...
自由分解(free resolution)是一種特殊的投射分解。設M是A模,若有正合序列:其中每個Fn都是A自由模,由序列(1)決定的投射分解稱為模M的自由分解。每個模M都有...
在上是有限型的,即:對任一點,存在其鄰域使得可由有限多個截面生成(換言之,存在正合序列)。對任意開集,任意及任意-模的態射,其核是有限型的。...
考慮導出函子的原始目的是從一個短正合序列造出一個長正合序列。具體言之:給定兩個阿貝爾範疇 ,及其間的加法函子 。假設 為左正合函子,換言之,對 中的任...
在數學中,更準確地是同調代數中,分裂引理(splitting lemma)說在任何阿貝爾範疇中,關於短正合序列的下列陳述是等價的。...
正合列是由交換群和同態組成的序列 ,並且它在每個交換群處正合,即 。內射分解短正合列 〔short exact sequence〕形如 的正合列稱為短正合列,此時f是單同態...
使得可由有限多個截面生成(換言之,存在正合序列 )。對任意開集 ,任意 及任意 -模的態射 ,其核是有限型的。環層 是凝聚層若且唯若它自身作為一個 -模是...
在同調代數中,蛇引理是構造長正合序列的關鍵工具,此引理在任何阿貝爾範疇中皆成立。依此構造的同態通常稱作連結同態。...
針對協定安全性驗證的複雜性,懷進鵬等證明了協定分析中所有正合序列空間可約簡為有限固定主體產生的正規序列空間,極大地縮小了需要分析的空間;證明了訊息無關時,...
正式地,N在M中的法叢是M的切叢的一個商叢: 我們有N上向量叢的短正合序列:這裡 是M的切叢限制在N上(準確地說,M的切叢 通過映射 拉回到N上)。 [1] ...
。由正合性, ,因 ,可以得到 為單射,則 ,再由正和性知 ,那么上述長正合序列可斷為: 。則拉格朗日-格拉斯曼流形的2階同倫群與O(n)基本群相同,即 。參考...
2.5 正合序列 2.6 混合張量 習題 第三章 張量代數 3.1 代數 3.2 對稱群 3.3 張量代數 3.4 對稱代數 3.5 外代數 3.6 斜稱張量 習題 第二...
群的分裂引理(splitting lemma)的一個版本稱群G同構於兩個群N和H的半直積若且唯若存在短正合序列和一個群同態r : H→ G 使得v o r = idH, H上的恆等...
在同調代數中,蛇引理是構造長正合序列的關鍵工具,此引理在任何阿貝爾範疇中皆成立。依此構造的同態通常稱作連結同態。 [1] 參考資料 1. MacLane, Saunders (1967...
投射分解是一種特殊的左復形,它是內射分解的對偶概念。設M是A模,M上的零調投射左復形稱為M的投射分解,它是一個正合序列。...
在阿貝爾範疇中相當於保存正合序列。3)忠實函子:使得對任意對象 , 為單射的函子。4)完全函子:使得對任意對象 , 為滿射的函子。...
由短正合序列的同構關係,可以定義群擴張的等價類。若某個群擴張等價於則稱此擴張為平凡擴張。當N落在G的中心時,稱之為中心擴張。 [1] ...
1.4.1模、同態與正合序列 1.4.2自由模與向量空間 1.4.3範疇與態射 1.4.4函子 1.5拓撲空間 1.5.1拓撲空間、拓撲基 1.5.2連續映射與同胚 1.5.3子空間、積空...
(3) 任何短正合序列 都分裂。(4) 函子 為正合函子。定義二:設R是一個環,E是一個R模。如果對於R模的任意單同態g: ,以及同態 ,f可以擴充為同態 ,...
