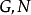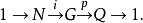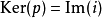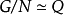振盪器代數

簡介

振盪器代數(oscillator algebra)也叫海森堡代數，是一種無限維復李代數，是一種無限維交換代數的中心擴張；可以用無限維Foch 空間上的微分運算元來表示，可以用來描述一部量子調和振盪器。

海森堡代數A是種復李代數，有基：

和交換關係式

其中

是中心元，可以任意交換。當

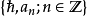
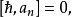
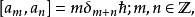
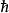
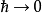
，A的極限就是交換代數。

數學上，李代數是一個代數結構，主要用於研究象李群和微分流形之類的幾何對象。李代數因研究無窮小變換的概念而引入。“李代數”（以索菲斯·李命名）一詞是由赫爾曼·外爾在1930年代引入的。在舊文獻中，無窮小群指的就是李代數。

在抽象代數中，設Q為群，若存在群

（換言之，i是單射、p是滿射，且

；是故可視N為G的正規子群，

。）則稱群G為Q的群擴張，或稱Q對N的擴張。

由短正合序列的同構關係，可以定義群擴張的等價類。若某個群擴張等價於

則稱此擴張為平凡擴張。當N落在G的中心時，稱之為中心擴張。