九引理

在數學中，九引理是一個對任意阿貝爾範疇（例如阿貝爾群範疇與模範疇）均成立的抽象結果，具體定義請參加正文。

基本介紹

• 中文名：九引理
• 外文名：Nine lemma

簡介

在數學中，九引理是一個對任意阿貝爾範疇（例如阿貝爾群範疇與模範疇）均成立的抽象結果，此引理斷言：給定如下的交換圖：

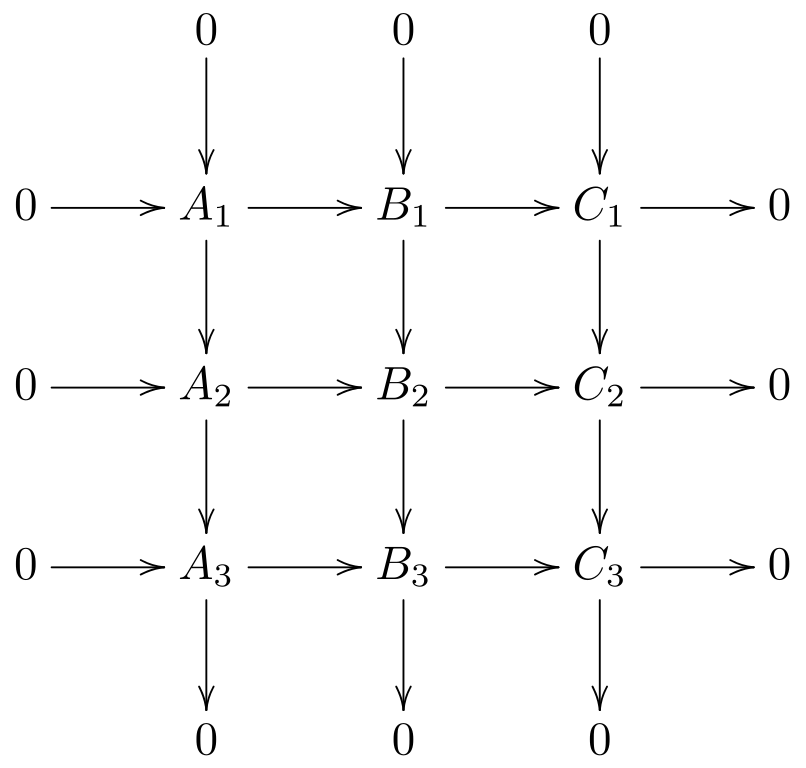圖1.

若每一直行及下兩橫列正合，則最上一個橫列也正合；類此，若每一直行及上兩橫列正合，則最下一個橫列也正合。

九引理可透過圖追蹤直接證明，或借著對正合橫列套用蛇引理證明。

阿貝爾範疇

在數學中，阿貝爾範疇（或稱交換範疇）是一個能對態射與對象取和，而且核與上核存在且滿足一定性質的範疇；最基本的例子是阿貝爾群構成的範疇Ab。阿貝爾範疇是同調代數的基本框架。

交換圖表

在數學領域，尤其是範疇論中，通常使用以對象為頂點、態射為邊的交換圖表來直觀的表達一些性質，尤其是泛性質。

在圖表中，複合連線任意兩個對象的不同路徑上的態射，所得的結果均相等，則稱此圖表可交換。同時，按照慣例，實線通常表示任意給定的態射，虛線則表示存在或唯一存在的態射。

蛇引理

在同調代數中，蛇引理是構造長正合序列的關鍵工具，此引理在任何阿貝爾範疇中皆成立。依此構造的同態通常稱作連結同態。