基本介紹
- 中文名:同調代數
- 外文名:homological algebra
- 創始人:昂里·嘉當、格羅坦迪克等
- 形成時間:第二次世界大戰後
- 所屬領域:數學
- 性質:一種代數方法
發展介紹
基本知識



















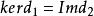







 圖1
圖1



















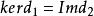







 圖1
圖1同調代數是隨著拓撲學,特別是同調論的發展而形成的一種代數方法。它把代數學中以往作個別研究的一些問題,用統一的觀點給予強有力的展開,而形成作為一般體系的領域...
《基本同調代數》是2003年6月1日由世界圖書出版公司出版的書籍。本書用英文介紹了基本同調代數的概念、作用、定理、運算方法、適用範圍等內容。...
《交換代數與同調代數》是 科學出版社 出版的一本圖書。...... 交換代數與同調代數編輯 鎖定 《交換代數與同調代數》是 科學出版社 出版的一本圖書。...
《同調代數方法》是2009年1月1日由科學出版社、科學出版社有限責任公司出版的圖書,作者是蓋爾范德、周伯壎。本書主要選取了國外的一些關於同調代數方法的數學理論知識...
《同調代數教程》是2003年出版的圖書,作者是P. J. Hilton、U. Stammbach。...... 1. 同調代數教程 .豆瓣讀書[引用日期2013-03-11 23:29:47] 詞條...
在數學中,伽羅瓦上同調是一套用群上同調研究伽羅瓦群的作用的技術。具體言之,假設伽羅瓦群 作用在一個群 (通常是數論中出現的代數結構,如 等等)上,伽羅瓦上同調...
《同調代數引論》是2011年2月大連理工大學出版社出版的圖書,作者是南基洙、王穎。...... 《同調代數導論》主要介紹證明Serre猜想的一些思想方法;第5章,群的擴張,初...
在數學中,霍普夫代數是一類雙代數,亦即具有相容的結合代數與余代數結構的向量空間,配上一個對極映射,後者推廣了群上的逆元運算。霍普夫代數以數學家海因茨·霍普夫...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。單純同調群是一個重要的拓撲不變數,它也是同倫型不變數。復形K的鏈...
代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個...
弱同調群(weak homology groups)是同調群的一種弱化。設K是復形,z和z′為K的兩個閉鏈,若存在非零整數m使得m(z-z′)同調於0,則稱z和z′弱同調。同調的...
《同調與同倫原理》是作者在代數拓撲選修課講義的基礎上,經仔細整理、增刪和潤色而成的。全書共分八章。第0章是對一般拓撲學基本理論的簡要回顧,第1、2兩章...
《環的同調維數》是程福長、易忠著,2000年10月廣西師範大學出版社出版的圖書。...... 本書可供學習過近世代數和同調代數基本知識的研究生和數學工作者參考。 [...
單純同調序列(simplicial homology sequence)是同調群所具有的一種性質。復形偶(K,L)與K和L的各種同調關係表現為它們的同調群組成的一個正合的序列,即單純同調...
單列代數(uniserial algebra)亦稱主理想代數。單側理想是主理想的特殊代數類。域F上有限維代數,其任意右理想或任意左理想都是主理想的代數稱為單列代數。單列...
模論是抽象代數學的重要組成部分之一,主要研究環上的模。模的概念本質上是域上向量空間的直接推廣。早在19世紀,狄利克雷(Dirichlet,P.G.L.)就曾經考慮過多項式...
單泛代數(simple universcal algebra)是一類特殊泛代數。若一個泛代數U僅有平凡契約關係,則稱U為單泛代數。...
抽象代數(Abstract algebra)又稱近世代數(Modern algebra),它產生於十九世紀。伽羅瓦〔1811-1832〕在1832年運用「群」的概念徹底解決了用根式求解代數方程的可能性...
實係數微分奇異同調群(differential singularhomology group with real coefficients)是邊緣運算元誘導的線性變換的核關於其像的商空間。對於每個p≥0,設∞Sp(M,R)表示...
結合代數(associative algebra):一種代數系統,類似於群、環、域,而更接近於環。結合代數的研究,早在19世紀50年代,W.R.哈密頓考察四元數、H.G.格拉斯曼引入向量...
內容簡介《國外數學名著系列(續1)(影印版)37:同調代數方法(第2版)》主要內容:Homological algebra first arose as a language for describing topological prospects...
在抽象代數中,在環上的模(module)的概念是對向量空間概念的推廣,這裡不再要求...它們還是交換代數和同調代數的中心概念,並廣泛的用於代數幾何和代數拓撲中。...
在抽象代數中,交換代數旨在探討交換環及其理想,以及交換環上的模。代數數論與代數幾何皆奠基於交換代數。交換環中最突出的例子包括多項式環、代數整數環與p進數環,...
《同調論》是2015年由北京大學出版社出版的圖書,該書作者是姜伯駒。該書共分五章,系統講述同調論的基本理論和方法。...
《數學概覽:代數基本概念》是I.R.沙法列維奇的經典名著之一,目的是對代數學、它的基本概念和主要分支提供一個一般性的全面概述,論述代數學及其在現代數學和其他...
代數幾何,是現代數學的一個重要分支學科。它的基本研究對象是在任意維數的(仿射或射影)空間中,由若干個代數方程的公共零點所構成的集合的幾何特性。這樣的集合通常...
代數K理論(的一個代數學分支。它的起源可追溯 到1958年格羅騰迪克(Grothendieck,A.)關於廣義 黎曼-羅赫定理的研究。這個學科的第一本專著是 1968年由巴斯(Bass...
代數拓撲法概述是拓撲學中主要依賴代數工具來解決問題的方法,同調與同倫的理論是代數拓撲方法的兩大支柱。龐加萊(H.Poincare)首先建立了可剖分空間的同調,艾倫伯格...
