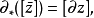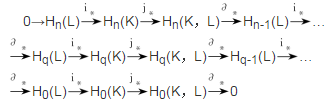單純同調序列

概念

同調群所具有的一種性質。復形偶(K，L)與K和L的各種同調關係表現為它們的同調群組成的一個正合的序列，即單純同調序列，它在單純同調論中有很多套用。設(K，L)是復形偶，其中K是n維復形，定義三種同態(為方便省去下標q)：

1.包含映射i：|L|→|K|誘導出同態

2.包含映射j：(|K|，)→(|K|，|L|)誘導出同態j_*：H_q(K)→H_q(K，L)。

3.聯繫同態_*：H_q(K，L)→H_q-1(L)，其定義為，設z'=z+C_q(L)∈Z_q(K，L)，其中z∈C_q(K)，∂z∈C_q-1(L)，z'的相對同調類記為[z']，z∈Z_q-1(L)，z在H_q-1(L)中的同調類記為[∂z]，若

則_∂*是一個同態，稱為(K，L)的同調聯繫同態，簡稱聯繫同態。

同調群與同態的序列：

稱為復形偶(K，L)的(單純)同調序列(或稱下同調序列)。它的重要特性是復形偶(K，L)的同調序列是正合的序列。類似可建立復形偶(K，L)的上同調序列，它也是正合的序列。

群是一種只有一個運算的、比較簡單的代數結構；是可用來建立許多其他代數系統的一種基本結構。

設G為一個非空集合，a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”，運算結果稱為“乘積”)滿足：

(1)封閉性，a·b∈G;

(2)結合律，即(a·b)c = a·(b·c);

(3)對G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，則稱G對於所定義的運算“·”構成一個群。例如，所有不等於零的實數，關於通常的乘法構成一個群;時針轉動(關於模12加法)，構成一個群。

滿足交換律的群，稱為交換群。

群是數學最重要的概念之一，已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱，就存在群。例如，可以用研究圖形在變換群下保持不變的性質，來定義各種幾何學，即利用變換群對幾何學進行分類。可以說，不了解群，就不可能理解現代數學。

1770年，拉格朗日在討論代數方程根之間的置換時，首先引入群的概念，而它的名稱，是伽羅華在1830年首先提出的。

交換群是指其運算適合交換律的群，或稱阿貝爾群。挪威數學家阿貝爾在研究高次方程的根式求解時，除了五次方程以外，他討論了更廣一類的方程，現稱之為阿貝爾方程。其全部根都是其中一個根的有理函式，設x1是n次阿貝爾方程的一個根，其全部根則為

，其中Qi(i=1，…，n-1)是有理函式，並且對於任意的1≤i≤j≤ n，有Qi(Qj(x1))=Qj(Qi(x1))。後人發現，阿貝爾方程是具有交換律的伽羅瓦群的方程。為了紀念阿貝爾，後人稱交換群為阿貝爾群。