基本介紹
- 中文名:單純同調群
- 外文名:pure homology group
- 領域:代數
- 性質1:重要的拓撲不變數
- 性質2:同倫型不變數
- 相關術語:弱同調群、上同調群
概念介紹
群
性質1——交換群
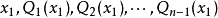
性質2——同倫
相關群
上同調群
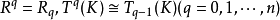
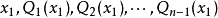
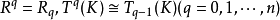
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。單純同調群是一個重要的拓撲不變數,它也是同倫型不變數。復形K的鏈...
單純同調序列(simplicial homology sequence)是同調群所具有的一種性質。復形偶(K,L)與K和L的各種同調關係表現為它們的同調群組成的一個正合的序列,即單純同調...
1 概念 2 拓撲空間 3 流形 4 拓撲流形 5 單純同調群 同調流形概念 編輯 同調流形(homology manifold)是一類重要的拓撲空間。設(X,A)為拓撲空間偶,若...
第1、2兩章是關於單純同調論的基本內容,主要介紹復形、單純映射和單純同調群等理論,它們將為第6章奇異同調論的學習,作適當“熱身”,並為學習第3章曲面的拓撲...
弱同調群(weak homology groups)是同調群的一種弱化。設K是復形,z和z′為K的兩個閉鏈,若存在非零整數m使得m(z-z′)同調於0,則稱z和z′弱同調。同調的...
由於Bn(K)是 Zn(K)的子群,把商群Zn(K)/Bn(K)叫做單純復形K的n維(下)同調群,記作Hn(K)。Hn(K)中的每一個元素叫做一個n維同調類。如果兩個n維閉鏈...
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態,...
3.3帶係數的胞腔同調與胞腔上同調 3.4單純復形與單純映射 3.5單純鏈復形與單純鏈映射 3.6有序單純復形 4胞腔同調的計算 4.1胞腔的定向 4.2胞腔鏈群的基 ...
第零章為預備知識,前三章介紹單純同調論,第四章為當前流行的範疇論。從第五章開始介紹在一般空間上的連續同調論,後四章是CW空間、一般係數的同調論、乘積空間的...
全書共分八章:拓撲空間的基本概念,緊緻性和連通性,商空間與閉曲面,同倫與基本群,復疊空間,單純同調及其套用,映射度與不動點等。每節配備了適量習題並在書末附...
類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈復形的同調序列等同調理論。從單純同調群和奇異同調群的理論可看出這些對象有許多共同特徵。 [1] 中文...
研究與同調概念有關的課題,如單純同調群、奇異同調群,上同調群及同調論公理、範疇與函子;②同倫論。研究與連續映射的連續形變有關的各種課題,如同倫問題、提升...
全書共分8章74節,內容豐富,論述精闢,主要內容包括單純同調群及其拓撲不變性、Eilenberg-Steenrod公理系統、奇異同調論、上同調群與上同調環、同調代數、流形上的...
重分和單純逼近存在定理;基本群定義及其同倫等價不變性、計算方法和一些計算結果的套用;在單純同調群之後介紹奇異同調群及其同倫等價不變性,同調群的正合序列、切除...
稱為復形K的q維上同調群,這些群中元素分別稱為上閉鏈、上邊緣鏈與上同調類。相應原來的同調群可稱為下同調群。設f:K→L是單純映射,f={fq:Cq(K)→Cq(L...
有向單形(oriented simplex)是建立同調群的重要概念。一個q維單形,它的q+1個頂點有(q+1)!個不同次序的排列,當q>0時,這些排列可分成兩組,同組的任意兩個...
《基礎拓撲學》是2010年04月人民郵電出版社出版的圖書,作者是阿姆斯特朗。該書主要講述了連續性、緊緻性與連通性、粘合空間、基本群、單純剖分、曲面、單純同調、...
奇藝同調群(singular homology group)是對任意拓撲空間都有定義的同調群。對每個非負數q確定一個q維單純形 ,稱為q維標準單形(standard simplex),記作△q。通常 ...
單純復形的n-階同調群的自由階等於n-階貝蒂數(Betti number),所以可以直接使用單純復形的同調群來計算它的歐拉特徵數。作為另外一個例子,閉流形的最高維的積分...
群的定義,球面的基本群,基本群的同倫不變性,基本群的計算,同倫提升定理與映射提升定理,復疊空間及其基本性質,復疊變換與正則復疊空間,單純復形的同調群,同調群...
