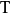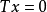簡介
同樣的,對於一個從
F線性空間V射到
F線性空間
W的
線性變換T:
T:
V→
W,
T的秩是它的象的
維度,
T的零化度是它的
核(
零空間)的維度。我們有:
也就是:
實際上定理在更廣的範圍內也成立,因為
V和
F可以是無限維的。
證明
設
V是一個有限維線性空間,
,對一個從
V射到
F的
線性變換 T,ker
T是
V的一個子空間。設 是 ker
T的一組基(
p≤
n)。根據基擴充定理,可以被擴充為
V的一組基:。 是一組
線性無關的向量,設
H是它們張成的子空間,那么
V是 ker
T與
H的直和:
所以,按照直和的性質,有
,並且,同時,,其中。考慮T限制在
H上到 im
T的
線性變換:
是一個
單射,因為, 。 是一個
滿射,因為, ,而且 ,其中。 於是 ,其中,所以是一個滿射。 於是是一個
H到 im
T的
同構,所以
證明[編輯]
設
是一個有限維線性空間,其維度
。對一個從
射到
的線性變換
,它的
核是
的一個子空間。設
是
的一組基
。根據基擴充定理,
可以被擴充為
的一組基:
。除了
的
個向量以外,另外的
個向量
是一組
線性無關的向量。設是它們張成的子空間,那么
是子空間
與
的直和:
所以,按照直和的性質,有
,並且這兩個子空間的交集為
。同時,
都可以寫成
的形式,其中
。考慮
限制在
上到
的線性變換
:
下證
是一個同構。首先由於
是線性映射,所以
是線性映射。只需證明它也是雙射:
是一個
滿射,因為
,
,使得
,而且
,其中
。 於是
,其中
,所以
是一個
滿射。
其他表達形式及推廣
正合列
是線性空間中的一個短正合列,那么有:
其中
R表示 im
T,
U表示 ker
T。 在有限維的情況下,上式可以作進一步推廣。如果
是有限維線性空間中的一個
正合列,那么有: 在有限維線性空間中,秩-零化度定理還可以用
線性變換的指標(index)描述。線性變換的指標指的是,對於線性變換
:
其中
表示
T的余核。正如 ker
T表示方程
線性無關的解的“個數”,
表示使得方程
有解而必須加於
y的限制條件的個數。
這時秩-零化度
定理表述為:
可以看到,在這種表述下,我們可以很容易地得到
T的指標,而不必對
T作深入研究。更深入的結果可以參見Atiyah–Singer指標定理(en:Atiyah-Singer index theorem)。Atiyah–Singer指標定理說明某些
微分運算元的指標可以通過涉及的空間的幾何性質得到。


 ,對一個從V射到 F的線性變換 T,ker T是 V的一個子空間。設 是 ker T的一組基( p≤ n)。根據基擴充定理,可以被擴充為 V的一組基:。 是一組線性無關的向量,設 H是它們張成的子空間,那么 V是 ker T與 H的直和:
,對一個從V射到 F的線性變換 T,ker T是 V的一個子空間。設 是 ker T的一組基( p≤ n)。根據基擴充定理,可以被擴充為 V的一組基:。 是一組線性無關的向量,設 H是它們張成的子空間,那么 V是 ker T與 H的直和:
 ,並且,同時,,其中。考慮T限制在 H上到 im T的線性變換:
,並且,同時,,其中。考慮T限制在 H上到 im T的線性變換:











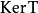



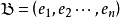








 ,並且這兩個子空間的交集為
,並且這兩個子空間的交集為 。同時,
。同時,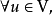 都可以寫成
都可以寫成 的形式,其中
的形式,其中 。考慮
。考慮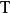 限制在
限制在 上到
上到 的線性變換
的線性變換 :
:

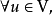


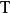





 是一個同構。首先由於
是一個同構。首先由於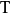 是線性映射,所以
是線性映射,所以 是線性映射。只需證明它也是雙射:
是線性映射。只需證明它也是雙射: