二元函子

二元函子(bifunctor)是範疇論以及同調代數、代數幾何等學科中常用的函子。若C₁，C₂，C為三個範疇，則從C₁，C₂的積範疇C₁∏C₂到C的函子稱為二元函子，同調代數中最重要的Hom函子等都是二元函子。

基本介紹

• 中文名：二元函子
• 外文名：bifunctor
• 所屬學科：範疇論以及同調代數、代數幾何等
• 相關概念：同調代數、積範疇、函子等

定義

二元函子(bifunctor)是範疇論以及同調代數、代數幾何等學科中常用的函子。若C₁，C₂，C為三個範疇，則從C₁，C₂的積範疇C₁∏C₂到C的函子稱為二元函子，同調代數中最重要的Hom函子、 函子等都是二元函子。

積範疇與二元函子

設C與D是兩個範疇，作範疇C×D如下:ob(C×D)=ob(C)×ob(D)，其中對象寫作(A,B)，A∈obC，B∈obD，對(A，B)∈ob(C×D)，A',B'∈ob(C×D)，規定Hom_C×D((A,B),(A',B'))=Hom_C(A,A')×Hom_D(B,B')，態射合成定義為(g,g')(f,f')=(gf,g'f')，恆等態射1_(A,B)=(1_A,1_B)。易驗證C×D也是範疇，稱之為範疇C與D的積範疇。

設F:C×D→E是乘積範疇到範疇E的函式，它對每個(A,B)∈ob(C×D)，給出F(A,B)∈obE，把C×D中的態射(f,g)變成E中的態射F(f,g)，並且任意給定A∈obC，則F(A,-):D→E是函子(或逆變函子)；任意給定B∈obD，也使F(-,B):C→E是函子(或逆變函子)，則稱F是二元函子。

正合二元函子

正合函子是阿貝爾範疇間的一種重要的函子，即保持短正合列的函子。設F：C→D為阿貝爾範疇間的一個共變函子，若對C中任意的正合列

有

是D中的正合列，則稱F為左正合函子，若對C中任意的正合列

有

是D中的正合列，則稱F為右正合函子，同時為左正合與右正合的函子稱為正合函子。對偶地，可定義反變函子的左、右正合性與正合性，若F為左(右)正合函子，則F變單(滿)態射為單(滿)態射且對任意的態射β，

左、右正合函子一定是加性函子。

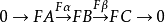
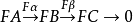
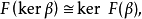
在同調代數的基本函子中(M表R模)，Hom(M，-)為左正合函子(它正合的充分必要條件是M為投射R模)；Hom(-，M)為左正合反變函子(它正合的充分必要條件是M為內射R模)；M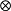-與-N(M為右R模，N為左R模)都是右正合函子(它們正合的充分必要條件是M(N)為平坦R模)；阿貝爾範疇中正向極限函子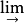(反向極限函子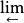)為右(左)正合函子。對二元函子F，若F關於它的兩個變元都是正合的(或左正合的、右正合的)，則稱F為正合的(或左正合的、右正合的)二元函子。

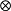
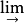
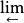
範疇論的Hom函子

範疇論的Hom函子(functor Hom in Category theory)亦稱共變態射函子或第一表示函子，範疇論中的重要函子之一，在同調代數中有著重要套用。設C為一個範疇，Set為集合範疇，對定義函子Hom_C(A，-):C→Set如下：

Hom_C(A，-)(X)=Hom_C(A，X) (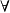X∈C)，

Hom_C(A，-)(f)：Hom_C(A，X)→Hom_C(A，Y)，

使Hom_C(A，-)(f)(g)=fg，f：X→Y在C中，g∈Hom_C(A，X)。這個Hom_C(A，-)稱為範疇C到Set的Hom函子。當C為加性範疇時，這個函子又是C到阿貝爾群範疇AG的函子，在同調代數中更顯出其重要性。