積範疇(product category)是範疇論的基本概念之一。指由一些範疇組成的新範疇。
基本介紹
- 中文名:積範疇
- 外文名:product category
- 領域:數學
- 學科:範疇論
- 定義:有一些範疇組成的新範疇
- 範疇論:代數學的分支
概念




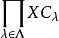
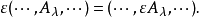
積範疇(product category)是範疇論的基本概念之一。指由一些範疇組成的新範疇。




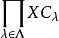
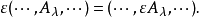
積範疇(product category)是範疇論的基本概念之一。指由一些範疇組成的新範疇。...... 積範疇(product category)是範疇論的基本概念之一。指由一些範疇組成的新範疇...
帶積範疇(category with product)是環上模範疇、有限生成投射模範疇等重要範疇關於直和及(交換環的情況下)張量積性質的抽象與概括。範疇是範疇論的基本概念之一。...
在數學中,範疇(category),是一種包含了對象及對象之間箭頭的代數結構。範疇具有兩個基本性質:一是對象之間的箭頭可以複合,且複合是滿足結合律的;二是每個對象到...
迴路範疇(loop category)一種重要的範疇.它由已知的帶積範疇考慮每個對象與其自態射所成的一種新的帶積合成範疇,它可以溝通K。群與K,群.設(x,y)為一個帶積...
纖維範疇(fibre category)一個帶積合成範疇.它是由兩個帶積範疇及它們之間的保積函子定義的.利用它可得到K。群、K群的有意義的正合列.設(x,y),,(z,e)...
共尾函子(final functor)是代數K理論中定義纖維範疇時用到的一類重要函子。它是一類特殊的保積函子。設(C,⊥),(D,⊥)為帶積範疇,F:C→D為保積函子。若...
二元函子(bifunctor)是範疇論以及同調代數、代數幾何等學科中常用的函子。若C1,C2,C為三個範疇,則從C1,C2的積範疇C1∏C2到C的函子稱為二元函子,同調代數中...
那么所稱的“軟體體積”,是對網路信息量大小的描述,也是常說的所占記憶體空間多少,既是描述空間大小那么就屬於體積範疇。計算機科學家沃思(Nikiklaus Wirth)早期提出...
