基本介紹
- 中文名:單純復形
- 外文名:Simplicial Complex
- 套用領域:數學
- 別稱:幾何單純復形
- 學科:單純同調論
- 作用:定義一類拓撲空間
拓撲學中的定義
 單純復形
單純復形單純同調論的定義
性質特點


 單純復形
單純復形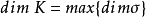


單純復形(Simplicial Complex)是拓撲學中的概念,指由點、線段、三角形等單純形“粘合”而得的拓撲對象。單純復形不應當與範疇同倫論中的單純集合混淆。單純復形...
復形是組合拓撲的基本概念之一,許多種拓撲空間的研究都可化歸為復形拓撲性質的研究,復形是不同維的正常分布的單純形之總和,即復形中任意兩個單純形,或不相交,...
單純逼近是與連續映射相關的單純映射。需要注意,並不是任何兩個復形的多面體之間的連續映射都存在單純逼近。...
數學裡,單純集合(simplical set)是範疇同倫論中一個構造,這是“良態”拓撲空間的一個純代數模型。歷史上,這個模型源自組合拓撲學特別是單純復形。...
抽象復形是幾何復形的一種抽象。將幾何單純復形的一些良好性質,利用同構復形的思想,加以抽象化就得到抽象復形的概念,同構的復形對應同一個抽象復形。...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。單純同調群是一個重要的拓撲不變數,它也是同倫型不變數。復形K的鏈...
復形偶(pair of complexes)特殊的一對復形.若K和L都是單純復形,LCK,則稱1.為K的子復形,IL}稱為!K}的子多面體,(K, 1.)與}IKI,IL I)分別稱為復形...
為區別起見,原來的單形可稱為無向單形。單純復形是幾何對象,而群是代數對象,從復形過渡到它的同調群,關鍵是單形的定向與邊緣運算元這兩個概念[1] 。...
若K是一個n維單純復形,Cq(K)是q維整係數鏈群,則同態c:Cq(K)→Z(整數加群)稱為K的一個q維上鏈。對於任意兩個q維上鏈c和d,它們的和是這樣的上鏈,它...
}取遍單純復形K的所有單形,且每個單形取好了定向(0維單形不取定向),αi為整數(即線性組合中的每一項是K中的一個n維定向單形,且附一個整係數)。兩個n維...
在純粹數學中,圖論被用來研究拓撲學中的單純復形,美國數學家維布倫在20世紀20-30年代就做出了先驅性的貢獻。他把一個圖定義為維數等於1或0的一個復形,1維單...
1 簡介 2 分片線性流形 組合流形簡介 編輯 對於其結構有限制的一類 PL 流形。設 是單純復形 K 中的一個單形, 為 在K 中的星形,它由K 中一切與 相交...
許多幾何體都可以通過單純復形—來建立模型,參見多胞形(Polytope)。 扎里斯基拓撲是一種純粹由代數來定義的的拓撲,這種拓撲建立在某個環的交換環譜之上或者某個...
對於一個以 A 為頂點集的抽象復形 𝓚,復形 𝓚 中的元素稱為復形 𝓚 的抽象單形。...
流形所使用的是彎曲的胞腔或圖形的小塊,人們今天所謂的單純同調的方法完全是龐加萊的創造:流形的三角剖分概念、單純復形概念、重心重分概念、對偶復形、復形的...
2 單純復形和單純映射3 抽象單純復形4 Abel群回顧5 同調群6 曲面的同調群7 零維同調8 錐的同調9 相對同調10 帶任意係數的同調...
在只定義在單純復形的單純同調之上,還可以使用光滑流形的微分結構來通過德拉姆上同調或Čech上同調或層上同調來研究定義在流形上的微分方程的可解性。德拉姆...
作為R的子空間稱為K的多面體,記為|K|,K稱為多面體|K|的一個單純剖分或三角剖分。一般地,多面體可以有不同的單純剖分.有限復形的多面體是緊緻空間。 [2] ...
《拓撲學基礎(第2版)》在介紹度量空間之後,引入拓撲空間,然後敘述拓撲空間的連續映射和同胚、緊緻性、連通性、乘積空間和商空間;從單形入手介紹單純復形和多面體的...
如同代數拓撲中的傳統作法,對它進行剖分,便產生能否剖分,以及不同的剖分是否等價等問題,因此引出分片線性結構的思想.設K K:為單純復形,對於映射f: IK} I-...
單純復形與多面體復形的同調形同調群的倫型不變性偽流形與Brouwer定理經濟學拓撲方法第三部分 微分拓撲學初步 第五章 微分流形與光滑映射...
2.2 r映射2.3 單純復形與CW復形2.4 收縮核與映射的可擴張性2.5 收縮核的某些繼承性質2.6 形變收縮核與鄰域收縮核第3章 絕對擴張子與絕對鄰域擴張子...
然後,可以把流形的歐拉示性數定義為一個和它同胚的單純復形的歐拉示性數。例如,圓圈和環面其歐拉示性數為0而實心球歐拉示性數為1。...
弱同調群(weak homology groups)是同調群的一種弱化。設K是復形,z和z′為K的兩個閉鏈,若存在非零整數m使得m(z-z′)同調於0,則稱z和z′弱同調。同調的...
2胞腔鏈復形與胞腔鏈映射 3胞腔同調定理 3.1胞腔同調定理 3.2胞腔同調定理的推論 3.3帶係數的胞腔同調與胞腔上同調 3.4單純復形與單純映射 3.5單純鏈復...
