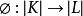單純逼近

單純逼近是與連續映射相關的單純映射。需要注意，並不是任何兩個復形的多面體之間的連續映射都存在單純逼近。

基本介紹

• 中文名：單純逼近
• 外文名：simplicial approximation
• 適用範圍：數理科學

簡介

設 K 和 L 是兩個單純複合形， 是連續映射， 是單純映射。如果對於 中容易一點 x ，點 在 L 中的承載單形是 在 L 中承載單形的面，即： ，則單純映射 稱為連續映射 f 的一個單純逼近。

有關單純逼近的一個重要命題是如下單純逼近的定理：對於單純複合形 K 和 L 的基礎拓撲空間之間的任何一個連續映射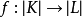，當正整數 n 充分大時，必存在一個單純逼近。

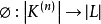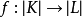
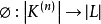
性質

當一個單純映射 是連續映射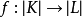的一個單純逼近時，對於中任意一點 x ，點在 L 中的承載單形包含了與兩點之間的連線。於是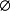，與 f 之間有一個線性同倫。這就是說，映射與它的任何一個單純逼近都是同倫的。由於和在 L 的同一個閉單純形中，和兩點的距離不大於 L 的網距。注意到有限單純復形的網距是有限的，給定有限單純復形 L ，當 m 趨於無窮時，單純復形 L 的 m 次重心重分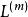 的網距趨於0。因此，將 L 重分足夠多次後，再利用單純逼近定理，可以得與給定連續映射任意接近的單純逼近。

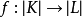
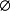
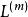
單純映射

(simplicial map)

單純映射是聯繫復形的多面體之間的一類重要映射。它是從復形K的多面體|K|到復形L的多面體|L|的連續映射，任何連續映射在某種意義下可用它逼近，可簡記為f：K→L(省去多面體|K|，|L|的記號)。單純映射是連續映射；單純映射由限制在頂點集上的映射f⁰=f|K⁰： K⁰→L⁰完全決定。反之，對於頂點集之間的任意映射f⁰，只要f⁰把K中任意單形的頂點集映成L中某單形的頂點集，它就惟一地確定一個單純映射f：K→L。