基本介紹
- 中文名:單純映射
- 外文名:simplicial map
- 屬性:聯繫復形的多面體之間的一類映射
- 所屬學科:數學
- 所屬問題:代數拓撲學
定義
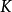
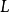
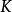



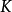
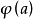



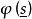

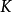
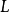


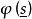



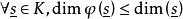
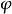

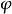

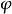

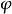

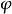

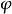



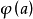
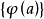
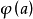

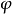
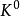


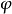



相關性質



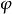
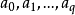

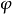







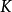
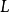
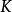



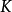
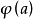



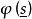

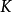
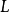


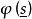



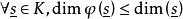
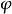





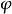



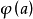
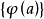
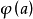

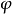
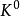


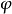






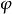
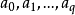

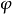






單純映射(simplicial map)是聯繫復形的多面體之間的一類重要映射。它是從復形K的多面體|K|到復形L的多面體|L|的連續映射,任何連續映射在某種意義下可用它逼近,可...
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態,...
單純逼近是與連續映射相關的單純映射。需要注意,並不是任何兩個復形的多面體之間的連續映射都存在單純逼近。...
數學裡,單純集合(simplical set)是範疇同倫論中一個構造,這是“良態”拓撲空間的一個純代數模型。歷史上,這個模型源自組合拓撲學特別是單純復形。...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。單純同調群是一個重要的拓撲不變數,它也是同倫型不變數。復形K的鏈...
反向映射機制是為了更新進程頁表項,使得更加有效地回收1個共享頁面,反向映射技術的實現主要是基於頁表項鍊表。...
分段線性映射指兩個單純形間的映射,它限制一個點(不是頂點)附近是線性的。 ...... 分段線性映射指兩個單純形間的映射,它限制一個點(不是頂點)附近是線性的。...
胞腔逼近定理(cellular approximation theorem)是代數拓撲學的一條重要定理。與單純逼近類似,CW復形之間的連續映射可以用胞腔映射來逼近。...
《基礎拓撲學》是2010年04月人民郵電出版社出版的圖書,作者是阿姆斯特朗。該書主要講述了連續性、緊緻性與連通性、粘合空間、基本群、單純剖分、曲面、單純同調、...
第六章 單純同調群(上)1 單純複合形2 單純複合形的同調群3 同調群的性質和意義4 計算同調群的實例第七章 單純同調群(下)1 單純映射和單純逼近...
單純映射與單純逼近,重心重分與單純逼近存在定理,連續映射誘導的同調群同態,同調群的同倫不變性,同調序列,球面自映射的映射度,保徑映射的映射度及其套用,Lefschetz...
