基本介紹
- 中文名:測地曲率
- 外文名:geodesic curvature
- 所屬學科:數理科學
- 相關概念:曲率、法曲率、Liouville公式等
定義,相關性質定理,定理1,定理2,定理3,
定義
設 為
為 正則曲面M上的曲線,
正則曲面M上的曲線,






相關性質定理
定理1
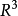


證明:將曲線C按法向n垂直投影到切平面 ,得到切平面上的一條曲面C*,這時投影直線就組成了一個柱面
,得到切平面上的一條曲面C*,這時投影直線就組成了一個柱面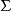 ,曲線C與C*都是柱面
,曲線C與C*都是柱面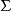 上過P點的曲線,它們的切向量都是T(因為C與C*都在柱面上,故它們的切向量都垂直於柱面的法向;另一方面,C在曲面M上,故它的切向量垂直M的法向量n;而由C*在切平面
上過P點的曲線,它們的切向量都是T(因為C與C*都在柱面上,故它們的切向量都垂直於柱面的法向;另一方面,C在曲面M上,故它的切向量垂直M的法向量n;而由C*在切平面 上,故C*的切向量也垂直M在P點的法向量n,由此推得C與C*在P點的切向量相同,都為T),因為TXn為柱面的法向量以及
上,故C*的切向量也垂直M在P點的法向量n,由此推得C與C*在P點的切向量相同,都為T),因為TXn為柱面的法向量以及 中向量
中向量 ,又因
,又因 ,故
,故 ,
, 平行於柱面
平行於柱面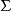 在P點的法向,於是,
在P點的法向,於是, 可視作曲線C在P點關於柱面的法曲率向量,所以對柱面運用Meusnier定理後知,
可視作曲線C在P點關於柱面的法曲率向量,所以對柱面運用Meusnier定理後知, 也為曲線C*關於柱面
也為曲線C*關於柱面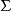 的法曲率向量,但C*又可視作柱面上過P點的相應於方向T的法截線,易知,
的法曲率向量,但C*又可視作柱面上過P點的相應於方向T的法截線,易知, 就是C*在P點的曲率向量(圖1)。
就是C*在P點的曲率向量(圖1)。

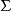
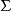






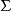


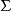

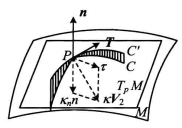 圖1
圖1定理2

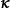


定理3
(Liouville)設M為 中2維
中2維 正則曲面,
正則曲面, 為其參數表示,並選
為其參數表示,並選 為正交的參數曲線網。令
為正交的參數曲線網。令






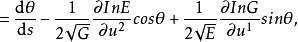


此外,還有