曲線在一點處的切向量可以理解為沿曲線該點處切線方向的向量。
切向量是與曲線相切的向量,給定曲線C上一點P,Q是C上與P的鄰近一點,當Q點沿曲線趨近於P時,割線PQ的極限位置稱為曲線C在P點的切線。
基本介紹
- 中文名:切向量
- 外文名:tangent vector
- 所屬領域:數理科學
- 定義:與曲線相切的向量
知識儲備



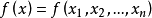











定義



相關概念介紹

例題解析
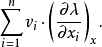

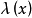
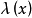








曲線在一點處的切向量可以理解為沿曲線該點處切線方向的向量。
切向量是與曲線相切的向量,給定曲線C上一點P,Q是C上與P的鄰近一點,當Q點沿曲線趨近於P時,割線PQ的極限位置稱為曲線C在P點的切線。



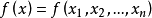















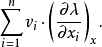

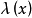
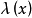

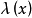

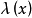
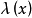
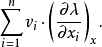





曲線在一點處的切向量可以理解為沿曲線該點處切線方向的向量。切向量是與曲線相切的向量,給定曲線C上一點P,Q是C上與P的鄰近一點,當Q點沿曲線趨近於P時,割線...
若某向量模數等於研究點處給定曲線的曲率,而該向量的方向與該點處曲線的主法線方向相同,則稱該向量為曲率向量。...
梯度向量場是由希爾伯特流形上的Cn泛函的梯度所形成的切向量場。梯度向量場生成的動力系統比較簡單,它們沒有周期軌,而且所有摩爾斯-斯梅爾梯度向量場(一類簡單的結構...
餘切向量是切向量的對偶概念。 流形M在點P處的切向量全體構成切空間,切空間的 對偶空間就是餘切空間。 餘切向量就是餘切空間中的向量。 粗略的說,餘切向量就是...
法向量是空間解析幾何的一個概念,垂直於平面的直線所表示的向量為該平面的法向量。由於空間內有無數個直線垂直於已知平面,因此一個平面都存在無數個法向量(包括兩...
雅可比向量場(Jacobi vector field)簡稱雅可比場.黎曼幾何的一個基本概念.一類重要的向量場.它是沿測地線滿足雅可比方程的向量場.雅可比場是指黎曼流形M上沿一條測...
數學中,流形 M 上一個向量值微分形式(vector-valued differential form)是 M 上取值於一個向量空間 V 的微分形式。更一般地,它是取值於 M 上某個向量叢 E ...
向量線(vector line)是向量場中具有特定意義的曲線,指其切線方向與場中向量一致的向量場中的曲線。設f是定義在區域Ω⊆R3上的向量場,Γ是Ω中的光滑曲線,若...
切空間是在某一點所有的切向量組成的線性空間。切空間是微分流形在一點處所聯繫的向量空間,歐氏空間中光滑曲線的切線、光滑曲面的切平面的推廣。切向量是切線的...
對空間曲線而言,空間曲線在某點的單位切向量和副法向量所張成的平面為空間曲線的從切平面。對研究空間曲線的性質有著重要意義。...
在向量微積分中,弗萊納公式(Frenet–Serret 公式)用來描述歐幾里得空間R中的粒子在連續可微曲線上的運動。更具體的說,弗萊納公式描述了曲線的切向,法向,副法方向...
在 的切向量為 ,其中t=h(s)。在E的切向量為 。因為x是s和 t的函式,而此處 t=h(s),局部求導有:類似地得 。因為E和 在該點相切,因此其切向量應平行,...
在代數拓撲中,毛球定理證明了偶數維單位球上的連續而又處處不為零的切向量場是不存在的。...
1 基本概念 2 定向曲線的參數方程 3 定向曲線的切向量 定向曲線基本概念 編輯 設L是一條與自身不相交的曲線(可以是封閉的曲線),當一動點沿曲線L連續地向同...
在的切向量為 ,其中 。在E的切向量為 。因為 是 和 的函式,而此處 ,局部求導有:類似地得因為 和 在該點相切,因此其切向量應平行,故有其中 。可用此兩式...
法截面是微分幾何的一個概念。曲面上一點,選定過該點的一個切向量,由該切向量和過該點的法向量所張成的平面,被稱為該切向量所決定的法截面。...
流形切叢(tangent bundle of manifold)一類最簡單的向量叢.微分流形上各點處的切向量的全體按自然方式做成的微分流形。...
