梯度向量場是由希爾伯特流形上的Cn泛函的梯度所形成的切向量場。梯度向量場生成的動力系統比較簡單,它們沒有周期軌,而且所有摩爾斯-斯梅爾梯度向量場(一類簡單的結構穩定的向量場)在所有梯度向量場是開稠的。
基本介紹
- 中文名:梯度向量場
- 外文名:gradient vector field
- 適用範圍:數理科學
定義






性質





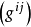


梯度向量場是由希爾伯特流形上的Cn泛函的梯度所形成的切向量場。梯度向量場生成的動力系統比較簡單,它們沒有周期軌,而且所有摩爾斯-斯梅爾梯度向量場(一類簡單的結構穩定的向量場)在所有梯度向量場是開稠的。











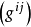

梯度向量場是由希爾伯特流形上的Cn泛函的梯度所形成的切向量場。梯度向量場生成的動力系統比較簡單,它們沒有周期軌,而且所有摩爾斯-斯梅爾梯度向量場(一類簡單的結構...
場論理論包括多種形式,比如簡單的向量場,而梯度場則是由數量場所得到的矢量場,它的定義與坐標系的選擇無關。梯度場在微分學、積分學以及運算元的定義方面起著重要...
梯度的本意是一個向量(矢量),表示某一函式在該點處的方嚮導數沿著該方向取得最大值,即函式在該點處沿著該方向(此梯度的方向)變化最快,變化率最大(為該梯度的...
重力位二階導數WXZ和WYZ表示重力場強度g在x和y水平方向的變化率,稱為重力場水平梯度。Ⅳ。WXZ和WYZ的向量和稱為重力場水平梯度向量,。 G=(W2XZ+W2YZ)1/2,...
梯度運算元編輯 鎖定 設某一給定正交坐標系的三個單位矢量為 ui ,而線元的平方可以表示為:ds 2 = gi dui2 ,那么體積元(其中 g = g1 g 2 g 3 )、dV ...
標量場的梯度是一個向量場。標量場中某一點上的梯度指向標量場增長最快的方向,梯度的長度是這個最大的變化率。更嚴格的說,從歐氏空間Rn到R的函式的梯度是在Rn...
場梯度,是不同時刻切向和法向溫度梯度等值線分布的現象。在航磁測量領域中,為了更好地顯示地質體構造走向及邊界位置,提出了地磁總場梯度的概念。地磁總場梯度不受...
梯度下降流(gradient descent flow)是由希爾伯特流形上泛函的負梯度向量場所生成的流。...
梯度:對於可微的數量場 ,以 為分量的向量場稱為f的梯度或斜量。[1] 梯度下降法(gradient descent)是一個最最佳化算法,通常也稱為最速下降法。...
在數學中,這些場可以表示為多元純量值函式或向量值函式,因而相應地稱這些函式為場,即把多元純量值函式稱為純量場(或標量場,數量場),多元向量值函式稱為向量場...
向量線(vector line)是向量場中具有特定意義的曲線,指其切線方向與場中向量一致的向量場中的曲線。設f是定義在區域Ω⊆R3上的向量場,Γ是Ω中的光滑曲線,若...
向量拉普拉斯運算元 均值在無窮小的球內向量場的值不同的程度 向量場的向量拉普拉斯是向量場 拉普拉斯運算元 對標量場 作梯度運算後,再作散度運算 標量場的拉普拉斯是標...
勢場(potential field)亦稱位場或梯度場一種特殊的向量場...... 勢場(potential field)亦稱位場或梯度場一種特殊的向量場 勢場(potential field)亦稱位場或梯度...
向量場、梯度場、散度場和旋度場共同構成了場論初步的基本內容,它既是高等數學曲面積分內容學習的理論基礎,同時也在物理學中發揮著重要的作用。由向量函式的旋度所...
旋度是向量分析中的一個向量運算元,可以表示三維向量場對某一點附近的微元造成的旋轉程度。 這個向量提供了向量場在這一點的旋轉性質。旋度向量的方向表示向量場在這...
如果一個矢量場是某個標量勢的梯度,那么便稱為保守矢量場。有兩個密切相關的概念:路徑無關和無旋矢量場。任何一個保守矢量場的旋度都是零(因此是無旋的),也...
J為擴散通量,為一個三維向量場,D為擴散係數,為一個二階張量,C為濃度,為一個數量場,▽為梯度運算元。上面兩個式子為菲克第一定律的數學表達式,它是描述擴散現象...
場勢是一種物理量,與力場有關,可為:標量勢;向量勢。...... 這情形類比於標量勢為一標量場,其負值梯度為一給定向量場。形式上,給定一向量場v,則向量勢為一...
另一類是第一個點對應著一個向量,這種場稱為向量場,如引力場、梯度場、電場、磁場。場本身的性質與坐標選擇無關,對各種場的分析和計算應該選擇適當的坐標系,以...
如果向量場v的旋度是零,這種向量場稱為無旋向量場,簡稱為無旋場。...... 如果一個向量場是某個標量勢的梯度,那么便稱為保守向量場。有兩個密切相關的概念:路...
