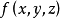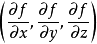梯度下降是疊代法的一種,可以用於求解最小二乘問題(線性和非線性都可以)。在求解機器學習算法的模型參數,即無約束最佳化問題時,梯度下降(Gradient Descent)是最常採用的方法之一,另一種常用的方法是最小二乘法。在求解損失函式的最小值時,可以通過梯度下降法來一步步的疊代求解,得到最小化的損失函式和模型參數值。反過來,如果我們需要求解損失函式的最大值,這時就需要用梯度上升法來疊代了。在機器學習中,基於基本的梯度下降法發展了兩種梯度下降方法,分別為隨機梯度下降法和批量梯度下降法。
基本介紹
簡介
求解過程
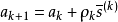


套用

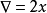











%% 最速下降法圖示% 設定步長為0.1,f_change為改變前後的y值變化,僅設定了一個退出條件。syms x;f=x^2;step=0.1;x=2;k=0; %設定步長,初始值,疊代記錄數f_change=x^2; %初始化差值f_current=x^2; %計算當前函式值ezplot(@(x,f)f-x.^2) %畫出函式圖像axis([-2,2,-0.2,3]) %固定坐標軸hold onwhile f_change>0.000000001 %設定條件,兩次計算的值之差小於某個數,跳出循環 x=x-step*2*x; %-2*x為梯度反方向,step為步長,!最速下降法! f_change = f_current - x^2; %計算兩次函式值之差 f_current = x^2 ; %重新計算當前的函式值 plot(x,f_current,'ro','markersize',7) %標記當前的位置 drawnow;pause(0.2); k=k+1;endhold offfprintf('在疊代%d次後找到函式最小值為%e,對應的x值為%e\n',k,x^2,x)

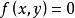
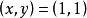
 圖1
圖1缺點
- 靠近極小值時收斂速度減慢。
- 直線搜尋時可能會產生一些問題。
- 可能會“之字形”地下降。