基本介紹
簡介

方法的表述
簡述

最後算法

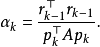
作為直接法
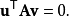



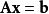
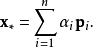
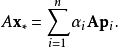
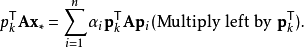



作為疊代法





例子

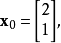

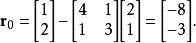
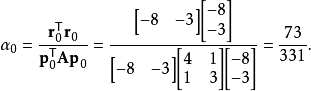
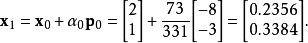









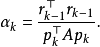
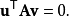



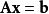
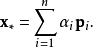
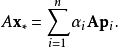
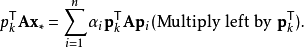









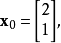

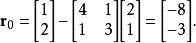
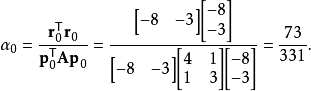
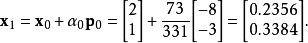





共軛梯度法(Conjugate Gradient)是介於最速下降法與牛頓法之間的一個方法,它僅需利用一階導數信息,但克服了最速下降法收斂慢的缺點,又避免了牛頓法需要存儲和計算...
定義介紹 預優共軛梯度法(preconditional conjugate gradiem method)亦稱預條件共扼梯度法.解線性方程組的有效方法之一它是基於共扼梯度法的收斂速度依賴於係數矩陣A...
定義 不完全喬萊斯基預優共轆梯度法(incompleteCholesky conjugate gradient method)簡稱ICCG方法.解大型稀疏對稱正定線性方程組的有效方法之一它是利用不完全喬萊斯基...
預處理共軛梯度法是。不必預先估計參數等特點。共軛梯度法近年來在求解大型稀疏方程組中取得了較好的成效。理論上普通的共扼梯度法對於對稱超正定方程,只要疊代步數...
最優解的基礎上提出的一類梯度型算法,包含共軛梯度法和變尺度法。根據共軛方向的性質,依次沿著對Q共軛的一組方向作一維搜尋,則可保證在至多n步內獲得二次函式的...
《預處理共軛梯度法識別橋樑動荷載分析與套用》是2014年中國水利水電出版社出版的圖書,作者是陳震。...
用共軛梯度法求解上述問題的算法為 ① 任選一個初始控制u0,且令i=0。 ②用ui從t0到tf求積狀態方程(1),得到xi(t),後再用ui和xi從tf到t0反向求積伴隨方程(...
梯度下降法(英語:Gradient descent)是一個一階最最佳化算法,通常也稱為最速下降法。 要使用梯度下降法找到一個函式的局部極小值,必須向函式上當前點對應梯度(或者...
梯度尋優,指沿某點函式變化率最小的梯度方向進行一維搜尋,求得該方向上的極小...梯度尋優參閱 編輯 共軛梯度法 隨機梯度下降法 參考資料 1. Mordecai Avriel ...
1 簡介 2 類型 ▪ 最速下降法 ▪ 共軛梯度法 下降法簡介 編輯 下降法亦稱極小化方法,是一類重要的疊代法。這類方法將方程組求解問題轉化為求泛函極小...
袁亞湘從事運籌學研究並取得了系統成果,在信賴域法、擬牛頓法、非線性共軛梯度法等方法方面做出了重要貢獻,在信賴域法算法設計和收斂性分析方面所做的工作是開創性...
在數值分析中用到疊代法的情形會比直接法要多。例如像牛頓法、二分法、雅可比法、廣義最小殘量方法(GMRES)及共軛梯度法等。在計算矩陣代數中,大型的問題一般會...
4.2 對正定二次函式的共軛梯度方法{99}4.3 非線性共軛梯度方法{105}4.4 數值試驗{110}4.5 Broyden 族方法搜尋方向的共軛性{112}...
2.22 條件梯度法2.23 共軛梯度投影法2.24 解決特殊形式函式緊緻集不適定問題的數值方法2.25 在源可表示情況下的不適定問題2.26 吉洪諾夫正則化方法...
4.4 共軛方向與線性共軛梯度法1794.4.1 共軛方向與擴張子空間定理1794.4.2 線性共軛梯度法與二次終止性1814.5 非線性共軛梯度法186...
常規的最佳化方法一般需要計算一階梯度,如最速下降法、共軛梯度法、變尺度法等,有些也需計算二階梯度,如牛頓法。由於計一算梯度值仍需對描述正問題的數學模型線性...
常規的最佳化方法一般需要計算一階梯度,如最速下降法、共軛梯度法、變尺度法等,有些也需計算二階梯度,如牛頓法。由於計算梯度值仍需對描述正問題的數學模型線性化,...
鬆弛法( relaxation method),是數值計算中解線性代數方程組的一類疊代法。逐次超...收斂都很慢,這就需要用一些輔助方法來加速收斂,例如半疊代加速、共軛梯度法加速...
若目標函式是多元函式,其最佳化方法有兩大類:①解析法(間接法):如梯度法、牛頓法、變尺度法和共軛梯度法等;②直接法:如坐標輪換法、模式搜尋法、方向加速法和...
3.4.6 極小化餘量法與GMRES方法3.5 截斷共軛梯度方法3.5.1 算法的提出3.5.2 算法的收斂性3.5.3 算法的正則性3.6 Lanczos方法3.7 預條件疊代方法...
目標協調法(goal coordination method)是處理大系統問題的一種基本分解、協調方法...步驟2:在第二級,用最速下降法或共軛梯度法來更新λ1(t)的軌跡,當總的系統...
3.5 截斷共軛梯度方法3.5.1 算法的提出3.5.2 算法的收斂性3.5.3 算法的正則性3.6 Lanczos方法3.7 預條件疊代方法3.8 正則參數選擇方法...
在數值分析中用到疊代法的情形會比直接法要多。例如像牛頓法、二分法、雅可比法、廣義最小殘量方法(GMRES)及共軛梯度法等。在計算矩陣代數中,大型的問題一般會...
