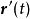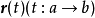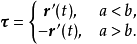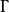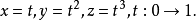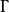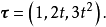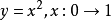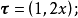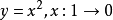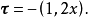定向曲線

定向曲線(oriented curve)亦稱有向曲線，指規定了方向的曲線。對曲線Γ：x=φ(t)，t∈[a，b]可以按參數增加(或減少)規定Γ的方向，即規定t₁<t₂(或t₂<t₁)時Γ上的點φ(t₁)在點φ(t₂)的前面。在前一情形，稱點φ(a)為Γ的始點，φ(b)為終點，由φ(a)到φ(b)的方向是正向；在後一情形則反之，閉曲線的始點與它的終點重合，曲線只有兩個方向，若取定其中之一為正向，則另一就是負向，正(負)向曲線常以Γ⁺(Γ^-)表示。設φ，ψ是曲線Γ的等價參數表示，即存在嚴格單調連續函式f，使ψ=φ°f，則當f嚴格增時稱f保持定向，這時Γ用φ，ψ表示的始點與終點一致，當f嚴格減時稱f反轉定向，對平面簡單閉曲線，通常按下列方法規定其正、負向：設曲線Γ在xy平面上，z軸與x，y軸形成右手坐標系，構想人站在xy平面上，抬頭的方向與z軸正向相同，若人沿Γ環行時Γ圍成的區域總在左手邊，則稱環行方向是正向，否則是負向。簡單地說，在右手坐標系中，反時針方向為正向，關於曲面或平面區域的邊界曲線的定向參見“雙側曲面”。

基本介紹

• 中文名：定向曲線
• 外文名：oriented curve
• 所屬學科：數學
• 別稱：有向曲線，定向曲線弧
• 簡介：指規定了方向的曲線

基本概念

設L是一條與自身不相交的曲線(可以是封閉的曲線)，當一動點沿曲線L連續地向同一方向移動時，該動點的移動方向就確定了曲線L的方向，我們稱確定了方向的曲線為定向曲線或定向曲線弧。一般地，一條定向曲線L的反向曲線記為L^-，若曲線L是以A為起點，B為終點的定向曲線，則記為 。對於定向曲線， 和 是兩條互為反向的定向曲線。

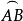
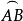
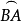
定向曲線的參數方程

定向曲線 也可寫為參數方程的形式

這裡用符號 表示變數t從a變到b，其中，t=a時對應的曲線上的點(x(a)，y(a)，z(a))是定向曲線 的起點A，t=b時對應曲線上的點(x(b)，y(b)，z(b))是定向曲線的終點B，定向曲線的參數方程也用如下向量形式表示

定向曲線的切向量

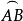
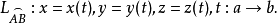
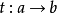
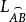
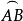
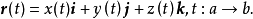
對光滑的定向曲線，其在任意一點處的切向量是指曲線在該點切線的方向向量中與曲線的方向一致的向量。

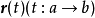
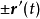
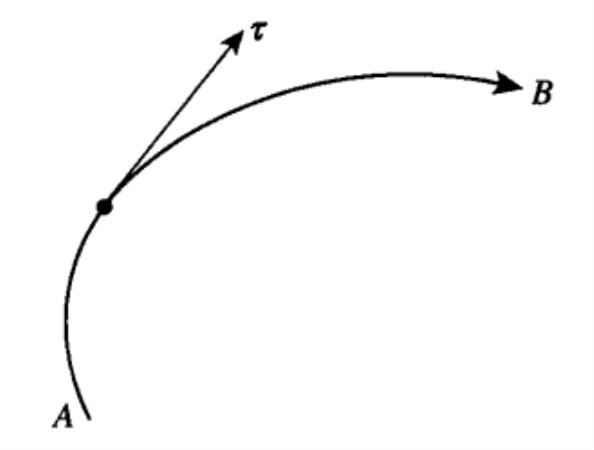
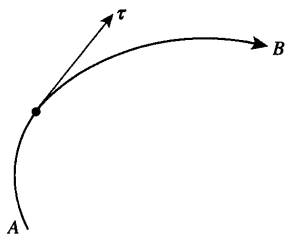圖1 曲線的定向與單位切向量

由一元向量值函式導數的幾何意義知，是曲線切線的方向向量中，方向指向參數增大的方向，所以定向曲線的切向量為

如空間定向曲線的參數方程為

則的切向量為

又如平面定向曲線L的方程為，則該定向曲線的切向量為

若定向曲線L的方程為，則其切向量為