法截面

法截面是微分幾何的一個概念。曲面上一點，選定過該點的一個切向量，由該切向量和過該點的法向量所張成的平面，被稱為該切向量所決定的法截面。

基本介紹

• 中文名：法截面
• 外文名：Law section
• 詞性：名詞
• 解釋：亦稱法平面
• 學科：微分幾何

概念

法截面亦稱法平面。包含曲面一點法線的所有平面。在大地測量學中常指包含地球橢球面一點法線的平面。過曲面上一點的法截面有無限多個。其中有兩個相互垂直且曲率半徑為極大和極小的法截面稱為主法截面。在地球橢球上，方位角為0°（180°）的主法截面稱為子午面；方位角為90°（270°）的主法截面稱為卯酉面。 法截線：法截面與曲面的截線。過曲面上一點的法截線有無限多條，其中兩個相互正交的主法截面與曲面的截線稱為“主法截線”。地球橢球面上，方位角等於0°（180°）的法截線稱為子午圈；方位角為90°（270°）的稱卯酉圈。過一點的所有法截線，其形狀都以過該點的子午圈和卯酉圈為對稱。

異形螺桿端截面與法截面關係研究

研究背景

螺桿泵轉子的加工國內主要採用成形法與無瞬心包絡銑削方法。使用成形法，用戶需要法面數據製作成型銑刀，成型銑刀沿螺旋線方向多次銑削形成多頭螺桿;使用無瞬心包絡銑削方法，用戶使用螺桿端面數據即可加工螺桿，同時用戶也可以使用成形銑刀檢測加工螺桿的形狀。無論使用哪一種加工方法，螺桿端面數據或法面數據是諸多生產廠家必需的前提數據，對端面數據與法面數據的研究在許多廠家來說是一個較複雜、困難的課題，一些廠家可能僅有端截面或法截面一種數據，所以實現這兩種數據的互相轉換對許多螺桿生產廠家來說是迫在眉睫的關鍵技術問題。

圖1 螺桿及其端截形示意圖

數學模型的建立

螺旋曲面的形成一般是在設螺桿的端面截形曲線為Γ(又稱為母線)時，讓該母線Γ繞以工件軸心Z軸為軸心線作螺旋運動所形成的曲面S。在工件坐標系中左旋螺旋曲面方程為：

圖2 平面曲線的切線和法線

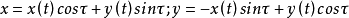
其中：t—參變數；τ—角度變數，表示母線Γ從起始位置繞Z軸轉過的角度，逆時針為正；p—螺旋參數，p=±h/2π，右旋螺旋面取“+”，左旋螺旋面取“-”。h為螺旋面導程，為已知參數(下面均以左旋為例)。圖1所示為5頭螺桿端面曲線形狀及螺桿。

如圖2所示，假設T、n分別是平面曲線c上M點的切線與法線，α為螺旋升角。為求得以參數方程式表達的曲面S上任意一點M的法線矢量n，可在曲面S上作一系列坐標曲線如圖3所示。現固定一個參數，例如令t=常數，得到曲面S上的一組空間曲線，稱為τ曲線。顯然，在τ曲線上，t=常數，只有參數τ變化；同樣可得與τ曲線相交的t曲線，t曲線上，τ=常數，只有參數t變化。這兩段曲線交織成曲面S。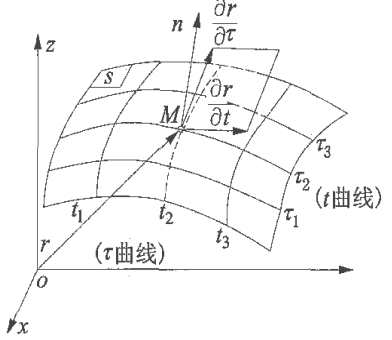

圖3 曲面的法線

研究結論

研究給出了螺旋曲面法截面與端截面相互轉換公式，通過在計算機上編程實踐並通過對實際數據進行檢驗，證明該轉換公式是正確的，已經在生產實踐中得到套用。

針對角鋼桁架的滿利用率齒行法截面最佳化

研究背景

對於桁架結構的最佳化，截面級的最佳化問題向來是遏制更高層次諸如形狀、拓撲最佳化的瓶頸，在文獻中研究者曾試圖用刪除大量不可行組合搜尋的方式尋求最優組合解，但在具體實施時，研究者還是放棄了全局組合方式。而同樣基於靜定化假設的思想，在疊代後的小片區域裡進行組合搜尋，這與經典滿應力設計方法在本質上是相似的。因此，在現階段，進一步研究滿應力思想是進行截面最佳化的必循之路。

相比於滿應力設計，滿利用率設計方法是一種以結構體系中每一桿件至少在一種工況下有一項或多項設計指標達到利用率最大為準則的最佳化設計方法。傳統的滿應力設計往往是針對連續截面變數而言的，以往的文獻也有將滿應力設計套用到設計變數為鋼管截面的桁架體系中。文獻提出的方法雖然可以達到滿應力最佳化的目的，但是效率比較低，而且僅僅照顧到應力約束，對於工程上應注意的長細比約束並未考慮。研究旨在提出一種比滿應力方法適應面更廣的滿利用率設計方法，借用成員設計變數的概念，同時針對非全截面對稱的角鋼桁架，綜合考慮應力及長細比約束，並採用齒行方式將設計值進行修正，將最佳化結果逼近到真實的最佳化解上。

算法思想

簡單的桁架結構體系的最佳化計算數學模型可以定義如下。

P₁：求I=[I_1，I_2，I_3，…，I_n]^T；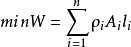

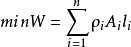
s.t. σ_i≤[σ_i+]，σ_i≥[σ_i-]λ_i≤[λ_i]，i = 1 , 2 , 3 , …, n

式中：I是設計變數截面對應於材料表中桿件截面的序號；ρ_i為材料密度；A_i為桿件截面積；l_i為桿件長度；σ_i與λ_i分別表示桿件應力和長細比；材料表S={s_1，s_2，s_3，…，s_m}；n為設計變數總數；m為離散截面型號總數。

角鋼材料表S中的一種截面型號包含了諸如肢寬b、肢厚t、面積A、最小軸迴轉半徑i_x、平行軸迴轉半徑i_y等多個信息，對於不同的約束條件所要用到的截面信息也不同。為了表示方便，這裡引入C++語言中類的成員變數的表示方法，分別以S_b、S_t、S_A、S_ix、S_iy表示某種型號角鋼的肢寬、肢厚、面積、最小軸迴轉半徑及平行軸迴轉半徑。這種表示方法可以很清楚地區分開同種截面型號中不同的信息類型，便於程式化操作。

含應力約束的截面最佳化問題的大基礎還是不能拋棄靜定化假設的，否則採用全搜尋法將會帶來令人難以忍受的時間耗用。滿利用率設計中的滿應力設計也是基於這個假設，也就是假定桁架內力重分析前後桿件剛度對各部分力的分配影響不大，從而對超靜定結構近似求取最優解。

對於靜定結構，由於約束條件是線性的，單根桿件的內力與其他桿件無關，利用疊代因子一次就可以達到最佳化目的。對於超靜定結構，由於靜定假設是對於一次疊代前後而言的，實際計算中疊代次數會因為約束條件的非線性而增多。如果結構的整體剛度矩陣為正常型(矩陣條件數很小)，則桿件內力的相互影響較小，疊代很快且能夠收斂到最佳化解上，疊代次數和結果不隨初始截面變化而變化；若結構的整體剛度矩陣為敏感型(矩陣條件數較大)，
則桿件剛度變化將導致疊代不容易收斂，這時候可以通過改變初始截面值的方法進行調整，但不同的初始截面可能會導致不同的疊代結果。因此，對於應力約束為最嚴約束的最佳化問題，結構的整體剛度矩陣為正常型是疊代能夠收斂的必要條件。工程實踐表明，絕大多數情況下輸電塔、空間桁架屋蓋等大型結構體系是屬於正常型的。類比文獻，可以提出滿利用率法的準則是各桿的疊代因子K=1。這裡綜合考慮了應力與長細比的雙重約束。另外，如果僅僅採用簡單的疊代方法，則設計變數只會在可行集與非可行集之間來回搜尋，最後在某些約束條件的交點上得到最優解。但最佳化設計的最優解往往不是位於某些約束條件的交點上，而是位於某一個約束曲線上。為了保證得到最優解，採用齒行路線法往往可以得到很好的效果。

齒行法與簡單疊代法的區別在於設計變數疊代到偶數步時，是從奇數步中得到各桿的K_i中選出最大的K_max作為各桿新截面的變更依據，嚴格意義上已不屬於滿應力設計的範疇，而是把每一步滿應力設計疊代公式作為更改設計減少重量的手段。這樣一來，對於在奇數步處於非可行集的有最嚴約束的桿件，在偶數步必定會回到約束曲面上來，而其他桿件則必定會退回可行集內。重複疊代以後，可以保證每次設計結果都會落在某個最嚴的約束曲面上，最終收斂到最優解而不再變化，從而達到最佳化設計的目的。

傳統意義上的滿應力法是針對連續設計變數而言的，文獻在離散設計變數的基礎上提出了擬滿應力設計的方法，這種方法簡單說來，是在每次應力重分析後，考察每根桿件的應力比程度，通過循環遞增或遞減桿件序號依次進行桿件截面驗算，選出滿足約束條件且應力比最大的桿件，從而達到物盡其用的目的。然而此種方法在桿件截面型號非常多的情況下勢必造成效率較低(組合角鋼材料庫截面類型可以高達100種以上)。借用應力比法思想，滿利用率設計可以將設計變數值快速鎖定在該疊代步最優離散截面值附近，此時比該計算值大的相應離散值所對應的材料型號就是該輪疊代的最優解。相比文獻的方法，將約束條件蘊含在疊代因子裡，省去每次疊代後各根桿件需要通過驗算遞增的繁瑣過程，大幅度提高了最佳化效率。

研究結論

根據上述算例可以看出，通過本文的最佳化思路可以達到最佳化目的，對滿利用率齒行法進行離散變數的截面最佳化總結如下。

(1)對於超靜定桁架組合變數的最佳化問題，可以採用全材料庫搜尋的方法得到最優解，但是相應犧牲的是時間(文獻曾經做過一個有趣的計算，假設截面庫只有3種材料，一共有60根桿件，單工況下，假設進行一次內力重分析需要1 μs，則完成一次全搜尋的計算時間會長達1.3×10¹³個世紀)。如果採用滿利用率齒行法，在設計值收斂的情況下，假設疊代1000次得到最優解，就算每根桿件每次循環比較時間與全部桿件內力重分析時間相同，總時間也不過61×1000=6.1×10⁴(μs)=0.061 s，加上讀寫檔案時間最多不超過1 s，最佳化效率顯而易見。在多工況下，這種時間優勢將更加明顯。

(2)離散截面最佳化設計的難點在於設計變數的離散性及大量的時間耗用，在最佳化過程中採用疊代因子可以有效地解決這2個問題。尋找最佳化疊代因子的關鍵是找到內力重分析前後的相關不變數，對於截面積為桿件內力，對於長細比為桿件長度。而對應力約束為最嚴約束的情況，超靜定假設對最佳化結果造成的約束一般是不能消除的，採用齒行法在一定程度上可以減小此種影響。

(3)滿利用率的基本思想是充分利用桿件的潛能，這對於桿件是多方面的，對於應力是面積潛能，對於長細比是迴轉半徑，對於局部穩定是寬厚比等。利用C++中類的思想可以將這些不同的信息區分開，也有利於將最佳化設計程式化。