在一定條件下,過曲面Σ上的某一點M的曲線有無數多條,每一條曲線在點M處有一條切線,在一定的條件下這些切線位於同一平面,稱這個平面為曲面Σ在點M處的切平面(tangent plane)。點M叫做切點。
基本介紹
- 中文名:切平面
- 外文名:tangent plane
- 拼音:qiē píng miàn
- 領域:幾何
性質
證明
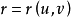
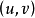


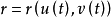
 球面的切平面
球面的切平面
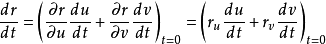





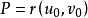

 切平面
切平面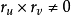

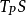

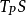

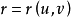
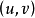
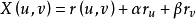
在一定條件下,過曲面Σ上的某一點M的曲線有無數多條,每一條曲線在點M處有一條切線,在一定的條件下這些切線位於同一平面,稱這個平面為曲面Σ在點M處的切平面(tangent plane)。點M叫做切點。
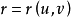
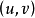


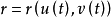
 球面的切平面
球面的切平面
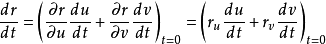


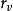
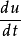
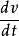

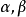


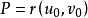

 切平面
切平面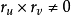

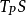

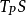

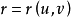
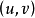
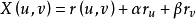
在一定條件下,過曲面Σ上的某一點M的曲線有無數多條,每一條曲線在點M處有一條切線,在一定的條件下這些切線位於同一平面,稱這個平面為曲面Σ在點M處的切平面...
割平面法主要用於求解整數規劃問題的方法。1958年由美國格莫理提出。基本思路是:先不考慮整數性約束,求解相應的線性規劃問題。若線性規劃問題的最優解恰好是整數解,...
中文名稱 吻切平面 英文名稱 osculating plane 定義 天體的瞬時位置矢量和速度矢量決定的平面。 套用學科 天文學(一級學科),天體力學(二級學科) 以上內容由...
不變平面是指對於無外力矩作用的定點運動,因角動量和能量守恆,慣量橢球在它與瞬時轉動軸交點處的切平面在空間中保持不變的取向,並且與定點保持不變的距離。因此這...
球與平面相切(contact between a sphere and aplane)球與平面的一種特殊位置關係.球與平面有且僅有一個公共點時,球與平面的位置關係...
在同一個平面上互相垂直且有公共原點的兩條數軸構成平面直角坐標系,簡稱直角坐標系(Rectangular Coordinates)。通常,兩條數軸分別置於水平位置與垂直位置,取向右與向上...
剖切面:製圖時,為了繪製剖視圖,用於剖切機件的假象的平面。分類:單一剖切面,平行剖切面,相交剖切面。...
剖面圖又稱剖切圖,是通過對有關的圖形按照一定剖切方向所展示的內部構造圖例,剖面圖是假想用一個剖切平面將物體剖開,移去介於觀察者和剖切平面之間的部分,對於...
斷面圖是在建築施工圖中,梁、柱、屋架、基礎等構件,我們用假想的剖切面將其割切開(按剖切符號所標註的位置),用正投影的方法,只將被剖切到的輪廓繪出剖切面,...
剖視圖 (Cutaway view 或者 Section view)剖視圖主要用於表達機件內部的結構形狀,它是假想用一剖切面(平面或曲面)剖開機件,將處在觀察者和剖切面之間的部分移去,...
剖切線是工程製圖術語,即在剖視圖中,用以表示剖切平面大小的圖線。...... 剖切線是工程製圖術語,即在剖視圖中,用以表示剖切平面大小的圖線。中文名 剖切線 ...
切空間是在某一點所有的切向量組成的線性空間。切空間是微分流形在一點處所聯繫的向量空間,歐氏空間中光滑曲線的切線、光滑曲面的切平面的推廣。切向量是切線的...
曲線在已知點處的測地曲率定義為它在切平面上的投影的曲率(圖5)。圖4 圖5 這樣一來,我們斷定平面幾何的基本概念都可以引進任意曲面的內蘊幾何中去。還很容易在...
