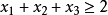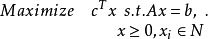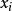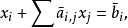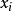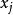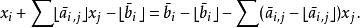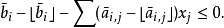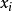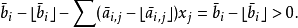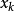割平面法主要用於求解整數規劃問題的方法。1958年由美國格莫理提出。基本思路是：先不考慮整數性約束，求解相應的線性規劃問題。若線性規劃問題的最優解恰好是整數解，則此解即為整數規劃問題的最優解。否則，就增加一個新的約束條件,稱為割平面。割平面必須具有兩條性質：（1)從線性規劃問題的可行域中至少割掉目前的非整數最優解；（2)不割掉任何整數可行域，然後在縮小的可行域上繼續解線性規劃問題。重複以上做法，經有限次切割後，必可在縮小的可行域的一個整數極點上達到整數規劃問題的最優解。
基本介紹
- 中文名：割平面法
- 外文名：cutting-plane method
- 別稱：切割平面法
- 提出者：高莫利(R.E.GoMory)
- 提出時間：19 世紀 50 年代
- 套用學科：數學
- 適用領域範圍：凸最佳化問題；混合整數線性規劃
簡介,Gomory 切割,基本步驟,基本思路,凸最佳化,
簡介
混合整數線性規劃（MILP）的割平面法通過將整數問題線性鬆弛為非整數線性問題，並對其進行求解，來求解 MILP 問題。線性規劃理論說明，在溫和的假定下（如果線性規劃存在最優解，並且可行域不包含一條線），總存在一個極值點或頂點是最優的。檢驗所獲的最優解是否為整數解。如否，則必然存在一線性不等式將最優點和真可行集的凸包分離。找到這樣的不等式是分離問題，而這樣的不等式就是切割。 切割可以被加入到被鬆弛的線性規劃中，使得當前的非整數解對鬆弛不再可行。該過程不斷重複，直到找到最優整數解。
用於普遍的凸連續最佳化和變體的割平面法有不同的名稱： Kelley 法， Kelley-Cheney-Goldstein 法和捆綁法。它們常用於不可微的凸最小化問題。對於這類問題，通常的可微最佳化的梯度法無法使用，而使用這些方法可以高效地得到凸目標函式及其次梯度。這種情況最常出現在雙拉格朗日函式的凹最佳化中。另一種常見情形是 Dantzig-Wolfe分解套用於結構最佳化問題中，這類問題通常有含有指數級變數的表達式。通過延遲列生成法按需生成這些變數等同於在對應的對偶問題上切割平面。
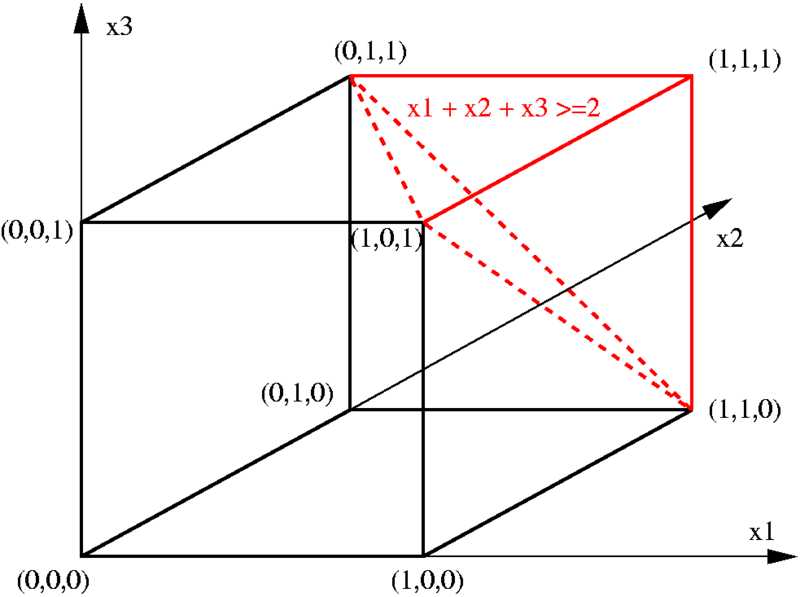圖1.割平面法例，如上圖1，單位立方體與切割平面
。 在三節點的旅行推銷員問題中，該（弱）不等式表明每次旅行必須連線至少兩個點。
Gomory 切割
切割平面法由 Ralph Gomory 在 19 世紀 50 年代提出，用於解決整數規劃和混合整數規劃問題。然而，當時的大多數專家，包括 Gomory 自己都認為由於數值上的不穩定性，這種方法沒有實際運用價值；同時由於求解過程中需要進行過多輪的切割，該方法可能是無效的。而在 19 世紀 90 年代中期，Gérard Cornuéjols 和同事發現切割平面法與分支定界法結合（稱作分支切割法）時效率很高，並且能有效克服數值不穩定性。現在，所有的商用 MILP 求解器都或多或少地使用了 Gomory 切割。Gomory 切割可通過單一單純形表格生成，相比於其他計算成本高昂、甚至分離為 NP-困難的其他切割法來說十分高效。在其他 MILP 的普遍切割法中，提升和投影割平面法明顯優於 Gomory 切割。
設一整數規劃問題被表達為其標準形式：
使用單純形法求解線性問題會產生一組如下形式的方程
所以上方的不等式排除了基本可行解，並且是符合需求的一次切割。通過將新的鬆弛變數
引入不等式中，新的約束得以加入到線性問題中：
基本步驟
在求解相應的線性規劃時，首先要將原問題的數學模型進行標準化。這裡的“標準化”有兩個含義：第一是將所有的不等式約束全部轉化成等式約束，這是因為要採用單純形表進行計算的緣故。第二是將整數規劃中所有非整數係數全部轉換成整數，這是出於構造“切割不等式”的需要。
(2)求一個“切割不等式”及添加到整數規劃的約束條件中去，即對上述線性規劃問題的可行域進行“切割”，然後返回步驟1。
基本思路
用割平面法求解整數規劃的基本思路是：先不考慮整數約束條件，求鬆弛問題的最優解，如果獲得整數最優解，即為所求，運算停止．如果所得到最優解不滿足整數約束條件，則在此非整數解的基礎上增加新的約束條件重新求解．這個新增加的約束條件的作用就是去切割相應鬆弛問題的可行域，即割去鬆弛問題的部分非整數解(包括原已得到的非整數最優解)．而把所有的整數解都保留下來，故稱新增加的約束條件為割平面．當經過多次切割後，就會使被切割後保留下來的可行域上有一個坐標均為整數的頂點，它恰好就是所求問題的整數最優解．即切割後所對應的鬆弛問題，與原整數規劃問題具有相同的最優解。
凸最佳化
切割平面法也適用於非線性規劃。 其基本原理是通過封閉半空間的有限集估算非線性（凸）問題的可行域，並對一系列的線性問題估算進行求解。
