曲面上的度量通過第一基本量可以表示為ds2=Edu2+2Fdudv+Gdv2。這裡E、F、G雖然是把曲面放在三維歐幾里得空間中求得的量,但是可以把它們看作曲面本身的(即與其所在空間無關的)量,並以此為基礎來建立幾何學。這樣,根據在曲面本身上定義的各種量來研究曲面的性質的數學分支,稱為曲面的內蘊幾何(intrinsic geometry)。當曲面無伸縮地變形時,其內蘊幾何不變。曲面的這種性質,稱為其內蘊性質。
基本介紹
- 中文名:內蘊幾何
- 外文名:intrinsic geometry
- 所屬學科:數學
- 相關人物:高斯、黎曼等
- 相關概念:內蘊性質、高斯曲率、測地曲率等
基本介紹,內蘊幾何學的興起,內蘊幾何的基本概念,
基本介紹
曲面的彎曲變形是指它保留曲面上曲線的長度不變的變形。舉例說,捲成筒狀的紙片從幾何觀點看來就是平面小塊的彎曲變形。事實上,這時曲面確實沒有伸展,而且畫在紙上的所有曲線的長度在捲起紙片時也沒有改變,保留不變的還有另外一些與曲面有關的幾何量,例如曲面上的圖形的面積,曲面在彎曲變形下不改變的所有性質,就組成曲面的所謂內蘊幾何的對象。
這是什麼樣的一些性質呢?顯然,在任意的彎曲變形下可以保留的只是那樣一些性質,它們只以有限步的計算依賴於曲線的長度,即它們可以用在曲面上所產生的測量方法來確定。彎曲變形是保留曲線長度的任意變形,而經過任何彎曲變形都不改變的每一個性質都可以這樣或那樣地通過長度來決定。大家說,內蘊幾何簡單地就是曲面上的幾何,“內蘊幾何”這名詞的本身的意義是說,研究的只是曲面本身的內在的性質,而不依賴於曲面在空間中是怎么樣彎曲的”。舉例說,如果我們在紙片上用直線段連結兩個點,然後彎曲這張紙(圖1),則線段就變成一條曲線,然而它是曲面上連結兩個已知點的最短曲線這個性質仍然保留;因此它屬於內蘊幾何,反之,這條曲線的曲率依賴於紙片的彎曲程度,因此已經不歸於內蘊幾何了。
 圖1(a)
圖1(a) 圖1(b)
圖1(b)一般地說,由於平面幾何的結論不牽涉到包容這個平面的空間的性質,平面幾何的全部定理都屬於從平面的彎曲變形所得到的任意曲面的內蘊幾何,可以說,平面幾何是平面的內蘊幾何。
內蘊幾何的另一個大家知道的例子是球面幾何,在測量地球表面時我們實質上就要用到它,這個例子特別適宜於說明內蘊幾何概念的本質。事實是,由於地球有很大的半徑而把直接看到的一塊地面理解成平的,因而在測量很大的距離時而觀察到的與平面幾何的差異就出現在我們面前,並非作為地球表面在空間中的彎曲的結果,而是作為由地球表面本身的幾何性質所表示的“地面幾何”所特有的法則。
 圖2
圖2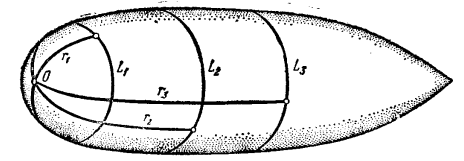 圖3
圖3應該指出,研究內蘊幾何的觀念本身當在高斯那兒產生時就是與測量學和地圖製圖學有關的。這兩種實用科學實質上都與地球表面的內蘊幾何有聯繫,地圖製圖學處理的特別是當把一部分地球表面畫到平面上時比例尺所受到的歪曲,因此也就要處理地球表面的內蘊幾何與平面幾何的差異。同理可以想像其他曲面的內蘊幾何:構想在已知曲面上生活著某種微小的生物,在這種生物的視界之內曲面看來像是平的(我們知道,任何平滑曲面的充分小的一片與切平面只有很小的差別);那么這種生物就不會注意到曲面是在空間中彎曲的,只有在測量較大的距離時,他們才會肯定他們的幾何學服從另外一些法則,這些法則正是相當於他們所生存的曲面的內蘊幾何的。至於這些法則確實隨曲面的不同而有差別,則可以用以下的論斷來肯定,在曲面上取一個點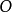 ,我們來討論這樣的曲線
,我們來討論這樣的曲線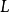 ,在曲面上量得的這曲線上的任意點到點
,在曲面上量得的這曲線上的任意點到點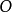 的距離(即連線這點與點
的距離(即連線這點與點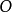 的最短曲線的長度)都等於常數
的最短曲線的長度)都等於常數 (圖2),曲線
(圖2),曲線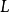 從內蘊幾何的觀點看來正是半徑
從內蘊幾何的觀點看來正是半徑 的圓周,用來表示曲線
的圓周,用來表示曲線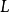 的長度
的長度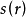 依賴於
依賴於 的公式是屬於已知曲面的內蘊幾何的,然而這種依賴關係卻可以是各種各樣的:例如在平面上
的公式是屬於已知曲面的內蘊幾何的,然而這種依賴關係卻可以是各種各樣的:例如在平面上 ;在半徑
;在半徑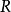 的球面上不難算出是
的球面上不難算出是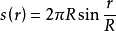 ;在圖3所畫的曲面上,從
;在圖3所畫的曲面上,從 的某個值開始,具有已知中心O的圓周的長度變得完全不依賴於
的某個值開始,具有已知中心O的圓周的長度變得完全不依賴於 ,而後來又變成遞減的。因此,以上所說的各種曲面具有不同的內蘊幾何。
,而後來又變成遞減的。因此,以上所說的各種曲面具有不同的內蘊幾何。
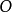
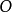


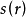


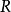
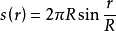


內蘊幾何學的興起
在高斯致力於微分幾何的研究(1827)之前,平面一直被作為三維歐幾里得空間中的圖形來研究。但是高斯表明,關於平面的幾何學能通過專注於平面本身得以研究。平面S 是具有兩個自由度的點的集合,因此S 上的任意一點r能用兩個參數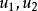 來表示。我們能獲得表達式:
來表示。我們能獲得表達式: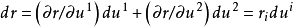 (
(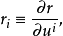 關於
關於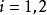 時的求和縮寫法),並且
時的求和縮寫法),並且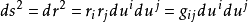 。高斯得出觀測結論: 平面的屬性,如弧長元、平面上兩條曲線之間的夾角,以及通常所謂的平面的高斯曲率,僅僅取決於
。高斯得出觀測結論: 平面的屬性,如弧長元、平面上兩條曲線之間的夾角,以及通常所謂的平面的高斯曲率,僅僅取決於 ,而這有許多推論。如果我們引人坐標
,而這有許多推論。如果我們引人坐標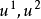 一這來源於:三維空間中平面的參數表示
一這來源於:三維空間中平面的參數表示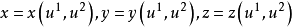 一併且運用由此確定的
一併且運用由此確定的 ,我們就獲得這個平面的歐幾里得性質。但是,我們能從這一平面出發,引人兩組參數曲線
,我們就獲得這個平面的歐幾里得性質。但是,我們能從這一平面出發,引人兩組參數曲線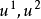 ,並用
,並用 作為
作為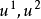 的函式而獲得
的函式而獲得 的表達式。因此,這一平面有一個由
的表達式。因此,這一平面有一個由 確定的幾何學。
確定的幾何學。
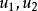
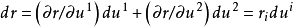
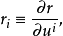
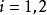
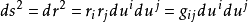

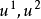
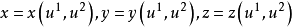

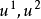

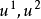


這一幾何學是內蘊於平面的,並且與周圍的空間沒有關係。這表明這個平面本身能被看作一個空間。如果這個平面本身被看作一個空間,那么它擁有什麼類型的幾何學呢? 如果我們認為那個平面上的“直線”是測地線( 平面上兩點間的最短連線),那么此幾何學可能是非歐幾里得的。因此,高斯的工作所隱含的是,至少在本身被看作空間的平面上有非歐幾何。
受高斯關於歐幾里得空間中平面的內蘊幾何學的引導,黎曼為一個種類更為寬泛的空間發展了一種內蘊幾何學(intrinsic geometry)(1854)。儘管三維幾何學顯然是重要的幾何學,但是黎曼更喜歡處理n維幾何學。他把n維空間當作一個流形來討論。在一個n維流形中的點由賦予n 個變元參數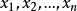 的特定數值,和構成n維流形本身的所有這些可能的點的總數表示。同高斯的平面內蘊幾何學一樣,黎曼流形的幾何學性質是用流形自身可確定的量來定義的,並且沒有必要把流形看作位於某種更高維的流形之中。
的特定數值,和構成n維流形本身的所有這些可能的點的總數表示。同高斯的平面內蘊幾何學一樣,黎曼流形的幾何學性質是用流形自身可確定的量來定義的,並且沒有必要把流形看作位於某種更高維的流形之中。
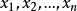
內蘊幾何的基本概念
為了說明內蘊幾何的概念和定理的範圍,讓我們來看一下作為平面的內蘊幾何的平面幾何。平面幾何的對象是平面上的圖形和它們的性質,這些性質通常是以長度、角度、面積等等基本幾何量之間的關係表出的。當然,角和面積屬於平面的內蘊幾何的嚴格的根據是在於:可以證明角和面積都能用長度來表出。這是因為,只要知道已知角所在的三角形各邊的長度,就可以算出這個角;三角形的面積也可以按它的各邊來計算,而任意多角形的面積則可以把它分成三角形來計算。
把平面幾何看作平面的內蘊幾何,並不必需限制在中學平面幾何的範圍。相反地,它可以展開得非常遠,加進新的問題,只要所引用的概念以有限次測量長度的計算作為基礎就成。例如在平面幾何里可以順次地引入曲線長度的概念,曲邊圖形面積的概念等等;它們全都屬於平面的內蘊幾何。
在任意曲面的內蘊幾何里可以引進同樣一些概念。曲線的長度在這時是原始的概念;至於角和面積情況稍有些複雜。假如已知曲面的內蘊幾何與平面幾何有差別,那么我們就不能按普通的公式用長度來決定角和面積。然而,我們曾經說過,曲面在已知點鄰近與其切平面很少差異。確切地說,下面的斷言成立:假如把包含已知點M的曲面小片投射到這點處的切平面上,那么在曲面上量得的兩點之間的距離與它們的投影之間的距離的差,比起它們到點M的距離來是高於二階的無窮小量。所以在決定屬於曲面的已知點的幾何量時,假如是用不高於二階的無窮小量為主的極限過程得到這些幾何量,則就可以把曲面的小片換成它在切平面上的投影。這時從切平面上量得的量對於曲面來說就是內蘊幾何的量。這種把曲面小片看作平面的可能性是定義內蘊幾何的所有概念的基礎。
作為例子,我們來討論角和面積的定義.依據一般的原則,曲面上曲線之間的角定義為它們在切平面上的投影之間的角(圖4)。顯然,用這種方法定義的角與曲線的切線之間的角重合。最後,為了刻畫曲線在曲面“內部”的彎曲需要引進測地曲率的概念;“測地曲率’這個名稱是從地球表面上的測量而來的。曲線在已知點處的測地曲率定義為它在切平面上的投影的曲率(圖5)。
 圖4
圖4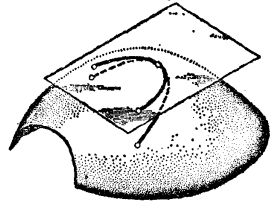 圖5
圖5這樣一來,我們斷定平面幾何的基本概念都可以引進任意曲面的內蘊幾何中去。還很容易在任意曲面上定義與平面上的基本圖形相仿的圖形。譬如說,我們已經談到過圓,它就可以像在平面上一樣來定義。還可以定義線段的同類物——“最短線”,作為曲面上連線兩個已知點的曲線中的最短者。然後,自然可以定義三角形(作為以三條最短線為界的圖形)、多角形等等。然而所有這些圖形和幾何量的性質都依賴於曲面本身,因而在這意義下就存在著無窮多種不同的內蘊幾何。但是內蘊幾何作為曲面理論的特殊部分,主要研究的是在任意曲面的內蘊幾何里都成立的那些一般的法則,而且在這時需要說明這些法則如何地通過刻畫已知曲面的幾何量而表示出來。
我們曾經指出過,曲面的最重要的特徵之一——它的高斯曲率——在彎曲變形下不變,即只依賴於曲面的內蘊幾何。原來高斯曲率就主要方面還刻畫了曲面在已知點鄰近的內蘊幾何與平面幾何的差異程度。作為例子,我們在曲面上討論以已知點O為中心而且有極小的半徑r的圓。在平面上這種圓的周長 出公式
出公式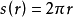 表示。在不同於平面的曲面上,圓周長度對半徑的依賴關係是另一個樣子的;這時可以證明,當r很小時,
表示。在不同於平面的曲面上,圓周長度對半徑的依賴關係是另一個樣子的;這時可以證明,當r很小時, 與
與 的差別主要依賴於圓心處的高斯曲率K,那就是說,
的差別主要依賴於圓心處的高斯曲率K,那就是說,

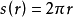


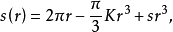
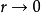
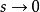
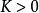

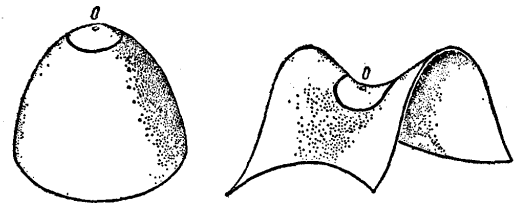 圖6
圖6從以上所引的定理推出,具有變動的高斯曲率的曲面是幾何地不均勻的,它的內蘊幾何的性質隨著點的改變而改變。如果說內蘊幾何問題的特徵使它接近於平面幾何,那么上述的不均勻性就成為它與平面幾何的很大的原則性的區別所在。譬如說,在平面上任何三角形的各角之和都等於兩個直角;而在任意的曲面上,由最短線組成的三角形的各角之和是不確定的,即使知道了三角形所在的曲面和指出了三角形的“大小”(例如各邊的長度)。然而,如果知道了在這三角形的每個點處的高斯曲率K,則它的各角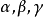 之和就可以按下列公式來計算:
之和就可以按下列公式來計算:
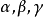
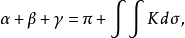
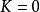
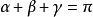
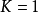

可以證明,高斯曲率為零的曲面的任何充分小的片段都可以彎曲(或者更常說成展開)到平面上,因為它有與平面相同的內蘊幾何,這種曲面叫做可展曲面。而如果高斯曲率接近於零,則雖然曲面已經不能展開到平面上,但是它的內蘊幾何與平面幾何只有很小的差別,這再一次表明,高斯曲率表示曲面的內蘊幾何與平面幾何的差異的程度。
測地曲線在內蘊幾何里起著直線的作用的是所謂測地曲線,它也常常簡單地叫做“測地線”。更多內容請參考相應參考書籍。

