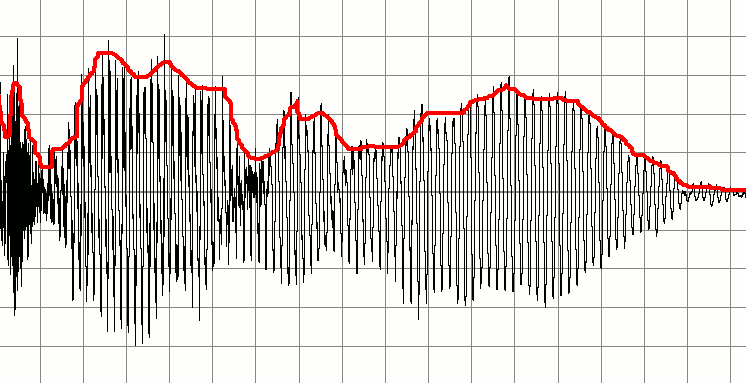
包絡函式(envelope function)是常見於電子工程領域,用來描述信號的一種特點。這種特點就是該信號的局部最大值的變化情況。
基本介紹
- 中文名:包絡函式
- 外文名:Envelope function
- 學科:數學
包絡函式的數學表示

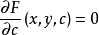
證明



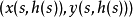



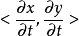
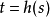



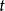





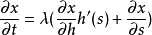




包絡函式(envelope function)是常見於電子工程領域,用來描述信號的一種特點。這種特點就是該信號的局部最大值的變化情況。

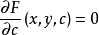




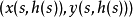



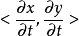
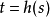








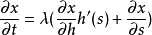




包絡函式(envelope function)是常見於電子工程領域,用來描述信號的一種特點。這種特點就是該信號的局部最大值的變化情況。...
包絡是由許多橢圓形曲線交織而成的一種圖形,外觀看起來是包起來的一樣。包絡在數學、信號處理、文學、經濟學、傳統中醫學上都有自己獨特的含義。...
在幾何學,某個曲線族的包絡線(Envelope),是跟該曲線族的每條線都有至少一點相切的一條曲線。(曲線族即一些曲線的無窮集,它們有一些特定的關係。)
頻譜包絡是將不同頻率的振幅最高點連結起來形成的曲線,就叫頻譜包絡線。頻譜是許多不同頻率的集合,形成一個很寬的頻率範圍,不同的頻率其振幅可能不同。計算頻譜...
羅蘭C接收的射頻脈衝包絡和其微分波形以適當比例相減後的波形。這樣合成的包絡在特定位置(例如高脈衝起點25μs處)有一個過零點,它用作包絡時差測量的基準點,還...
包絡代數(enveloping algebra)是代數幾何中的重要概念,是指由給定代數與其反代數...若一個代數簇V1到另一個代數簇V2的映射誘導了函式域之間的同構,則稱該映射為...
語音頻譜包絡中文意思:語音頻譜包絡是語音合成技術的重要組成部分。 在數學上,“包絡”(envelope)是指一系列的直線(或曲線)包圍出一個形狀的情形。例如直線組成一個...
下包絡原理是描述兩個位勢的下確界仍是位勢的一個原理。所有的α核都滿足下包絡原理。...
在測距定位系統中,為了有效的抑制帶外的干擾,系統都具有帶通特性。典型的帶通系統都具有色散特性。信號包絡經過系統後產生的失真稱為包絡失真,所產生的時延稱之為...
成本函式(cost function)指在技術水平和要素價格不變的條件下,成本與產出之間的相互關係。成本理論主要分析成本函式。成本函式和成本方程不同,成本函式說的是成本和...
次線性函式(sublinear function)是一類重要的凸函式。正齊次且是次可加的函式稱為次線性函式。局部凸空間(包括賦范線性空間、有限維空間)上的下半連續次線性函式...
135極大值函式和包絡定理13.6對偶和包絡定理137一些結論性評論第五篇 動態分析第14章 動態經濟學與積分學14.1動態學與積分14.2不定積分...
