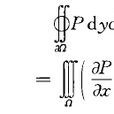高斯-奧斯特羅格拉茨基公式

高斯-奧斯特羅格拉茨基公式(Gauss-Ostro-gradsky formula)簡稱高一奧公式，亦稱散度定理、高斯公式、高斯散度定理，是指在向量分析中，一個把向量場通過曲面的流動（即通量）與曲面內部的向量場的表現聯繫起來的定理。

基本介紹

• 中文名：高斯-奧斯特羅格拉茨基公式
• 外文名：Gauss-Ostro-gradsky formula
• 別稱：高斯散度定理；高斯公式
• 提出者：高斯
• 學科：數理科學

概念

高斯-奧斯特羅格拉茨基公式是指在向量分析中，一個把向量場通過曲面的流動（即通量）與曲面內部的向量場的表現聯繫起來的定理。

更加精確地說，散度定理說明向量場穿過曲面的通量，等於散度在曲面圍起來的體積上的積分。直觀地，所有源點的和減去所有匯點的和，就是流出這區域的淨流量。

高斯-奧斯特羅格拉茨基公式在工程數學中是一個很重要的結果，特別是靜電學和流體力學。

在物理和工程中，散度定理通常運用在三維空間中。然而，它可以推廣到任意維數。在一維，它等價於微積分基本定理；在二維，它等價於格林公式。

這個定理是更一般的斯托克斯公式的特殊情形。

定理

設空間閉區域Ω是由分片光滑的閉曲面Σ所圍起來的三維區域，函式P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一階連續偏導數，則有

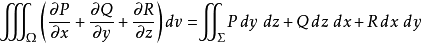
或

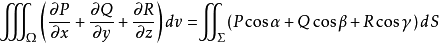
這裡Σ是Ω的邊界，cos α、cos β、cos γ是Σ在點(x,y,z)處的單位法向量的方向餘弦。

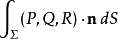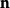這兩個公式都叫做高斯公式，不過這兩公式僅僅是表達方式不同，其實是相同的定理，這可以用變數變換得到兩公式的右邊都等於，其中 是曲面 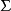的向外單位法向量。

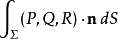
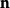
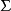
用散度表示

高斯公式用散度表示為：

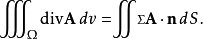
其中Σ是空間閉區域Ω的邊界曲面，而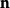是曲面Σ上的朝外的單位法向量。

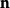
用向量表示

令V代表有一間單閉曲面S為邊界的體積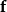，是定義在V中和S上連續可微的向量場。如果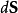是外法向向量面元，則

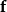
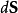
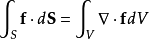
推論

對於標量函式g和向量場F的積，套用高斯公式可得：

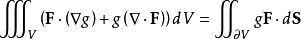
對於兩個向量場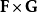的向量積，套用高斯公式可得：

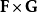
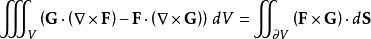
對於標量函式f和非零常向量的積，套用高斯公式可得：

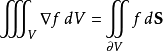
對於向量場F和非零常向量的向量積，套用高斯公式可得：

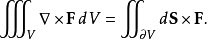
例子

假設我們想要計算

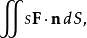
其中S是一個單位球面，定義為

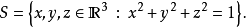
F是向量場

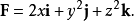
直接計算這個積分是相當困難的，但我們可以用高斯公式來把它簡化：

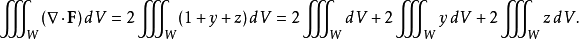
其中W是單位球：

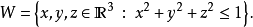
由於函式y和z是奇函式，我們有：

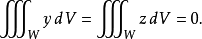
因此：

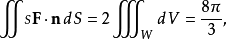
因為單位球W的體積是4π3.