奧斯特羅格拉茨基方法簡稱奧氏方法。一種直接求出有理函式積分的有理部分的方法。這種方法是奧斯特羅格拉茨基 (Ocтpoгpaлcкий,M.B.)於 1845 年發表的。
基本介紹
- 中文名:奧斯特羅格拉茨基方法
- 外文名:Ostrogradski method
- 適用範圍:數理科學
簡介
內容


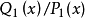
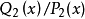
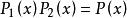
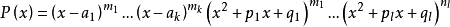

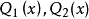
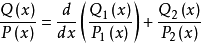

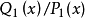

奧斯特羅格拉茨基方法簡稱奧氏方法。一種直接求出有理函式積分的有理部分的方法。這種方法是奧斯特羅格拉茨基 (Ocтpoгpaлcкий,M.B.)於 1845 年發表的。


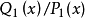
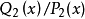
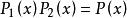
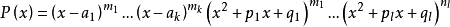

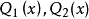
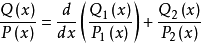

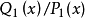

奧斯特羅格拉茨基方法簡稱奧氏方法。一種直接求出有理函式積分的有理部分的方法。這種方法是奧斯特羅格拉茨基 (Ocтpoгpaлcкий,M.B.)於 1845 年發表的...
高斯-奧斯特羅格拉茨基公式(Gauss-Ostro-gradsky formula)簡稱高一奧公式,亦稱散度定理、高斯公式、高斯散度定理,是指在向量分析中,一個把向量場通過曲面的流動(即...
奧斯特羅格拉茨基,M.B.,俄國數學家、力學家。1801年 9月24日生於帕先納亞,1862年1月1日卒于波爾塔瓦。早年在哈爾科夫大學學習,雖然成績優異,但由於不信教而未...
奧斯特羅格拉茨基(Ostrogradsky,Mikhail Vasilievich;1801~1862)俄國數學家,物理學家。1801年9月24日生於帕先納亞,1862年1月1日卒于波爾塔瓦。早年在哈爾科夫大學...
《數學分析》的全部命題,但該書習題數量多,許多題目在題型和解題方法上具有相似...§16.奧斯特羅格拉茨基公式§17.場論 [1] 參考資料 1. 吉米多維奇數學分析...
羅巴切夫斯基創造性地運用了處理複雜數學問題常用的一種邏輯方法——反證法。這種...“寬容”的話,那么,奧斯特羅格拉茨基則使用極其挖苦的語言,對羅巴切夫斯基作了...
用奧斯特羅格拉茨基法求積(習題1890–1902)39 3.2.3 雜題(習題1903–1925)44 §3.3 無理函式的積分法(習題1926–1990)47 3.3.1 用有理化方法求積(習題...
16.奧斯特羅格拉茨基公式 17.場論初步 [2] 參考資料 1. 吉米多維奇數學分析習題集題解6 .豆瓣讀書[引用日期2013-04-30] 2. б.п.吉米多維奇數學分析習題集...
徹底解決了奧斯特羅格拉茨基不久前才提出的一類代數無理函式的積分問題,他因此被提升為高等代數與數論講師.他在文章中提出的一個關於二項微分式積分的方法,今天可以...
問題和解決問題的能力,特別是對部分難題的研讀,可以幫助掌握綜合分析的思維方法。...14.曲面積分 15.斯托克斯公式 16.奧斯特羅格拉茨基公式 17.場論初步 [1] 參考...
(Обинтегрировaниисномошьюлогaрифмов, 1847) 的晉職報告中,切比雪夫徹底解決了奧斯特羅格拉茨基不久前才提出的一類...
原來他創造性地運用了處理複雜數學問題常用的一種邏輯方法——反證法。 這種反證...“寬容”的話,那么,奧斯特羅格拉茨基則使用極其挖苦的語言,對羅巴切夫斯基作了...
的唯心主義觀點.此外,他在物理學、力學和天文學方面也有許多著作.他還培養了許多優秀人才,其中有奧斯特羅格拉茨基(OcTporpa,qcxHH,M. B.)等人....
聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 加...另一方面,奧斯特羅格拉茨基(М.В.Остроградский)證明了,如果...
應力、應變狀態的變化以波的方式傳播,稱為應力波。通常將擾動區域與未擾動區域...奧斯特羅格拉茨基、G.G.斯托克斯等人,以及隨後由瑞利等人研究與彈性振動相聯繫的...
解或"有限形式的" 解, 所以使學生熟悉近似方法的運用與學會作出近似公式都有其...167. 奧斯特羅格拉茨基的積分有理部分分出法 249 x3. 某些根式的積分法 251...
1918年 - А. А. 奧斯特羅格拉茨基(А. А. Остроградский)圖集 狄安娜號防護巡洋艦圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數...
35.奧斯特36.歐姆37.法拉第38.貝爾39.羅巴切夫斯基40.賴爾41.奧斯特羅格拉茨基42.楞次43.達爾文44.皮羅果夫45.季寧46.亥姆霍茲47.孟德爾...
19世紀初,數學家們投入了無窮無盡的精力,他們幾乎嘗試了各種可能的方法,但都...科學院委託著名數學家奧斯特羅格拉茨基院士作評定。奧斯特羅格拉茨基是新推選的...
治學方法,概括性地論述了微積分的萌芽、創建、發展過程,其中還包含了一些科學家...奧斯特羅格拉茨基阿貝爾雅可比狄利克雷哈密頓劉維爾李善蘭魏爾斯特拉斯...
斯米爾諾夫曾長期領導物理-數學史委員會工作,為出版經典數學家的著作和俄國數學家如奧斯特羅格拉茨基,李雅普諾夫,克雷洛夫等的著作做出很大努力。斯米爾諾夫的著作以《...
解決了奧斯特羅格拉茨基不久前才提出的一類代數無理函式的積分問題,他因此被提升為高等代數與數論講師.他在文切比雪夫章中提出的一個關於二項微分式積分的方法,...
變元函式使泛函達到極值的必要條件和充分條件,並研究求得該變元函式的方法及其...、奧斯特羅格拉茨基(Остороградский,М.В.)、德洛內(...
