圖基引理

圖基引理(Tukey's lemma)是選擇公理的一種等價形式，設有集合之集A，若任一集合A屬於該集A，若且唯若集合A的每個有窮子集都屬於該集A，則稱集A具有有窮特徵。例如，一給定線性空間的所有線性無關組構成的集即具有有窮特徵。圖基引理斷言，每個具有有窮特徵的非空集必有集合之間包含關係下的極大元，可以證明，圖基引理與佐恩引理等價，因而也與選擇公理等價，因為有許多概念是用有窮性質定義或由有窮時的性質推廣至無窮的，所以，要斷言極大元的存在性，使用圖基引理就甚為方便了，證明“任一線性空間都有基底”即是例證。

基本介紹

• 中文名：圖基引理
• 外文名：Tukey lemma
• 別稱：第二極大原理
• 所屬學科：數學（集合論）
• 簡介：選擇公理的一種等價形式

基本介紹

圖基引理(Tukey lemma)亦稱第二極大原理，集合論的一條重要引理，它與選擇公理等價，由圖基(J.W.Tukey)於1940年獨立提出，該引理斷言：若C是關於集合的有限特徵條件，則集X中所有滿足條件C的子集中，至少有一個滿足條件C的極大元素。

選擇公理是Zermelo(1904)為證明整序定理而提出來的，這對近代數學理論的發展和邏輯上的嚴密性起了大為推進一步作用。Vitali(1905)利用它造出了[0，1]中的不可測集合；Zorn(1935)又用它證明了第一極大原理(即Zorn引理)，這個原理是套用起來最方便而特別受人歡迎的；Teichmüller(1939)與Tukey(1940)又提出了第二極大原理(通常又稱為Tukey引理)。

圖基引理的證明

Zorn引理如果部分序集A的每個序子集均在A中有上界，則A必含極大元素。

Zorn引理也稱第一極大原理。

圖基引理的證明：

Tukey引理 具備有限特徵性的非空類F恆含極大元素。

證明：在F中任取一個序子類C來看，令

即A為C中所有集合之並集，則由F的有限特徵性易知必有A∈F，於是A就是C在F中的一個上界，故由Zorn引理即知F含極大元素。 證畢。

相關定理

定理 下列諸命題等價：

1.選擇公理；

2.整序定理，

3.Zorn引理；

4.Tukey引理。

證明：用循環證法。

12。不妨設S為任意非空集合。令f為S的冪集合US上的一個選擇函式。再令

假設對所有小於σ的序數v已定義了a_v，則可定義

這樣定義盡S的元素後，S即成整序集

了(本證明也可以看作是獨立於以前所推導出的結果，如Zorn引理與整序定理等，這隻要認為是在Von Neumann所大力發展起來的序數理論上來看待問題就成了。所以對初學者來說， 如果感到Zorn引理與整序定理的證明太長而費解時，則可以先跳過去，就只看這裡的較為簡短的統一論述就行了)。

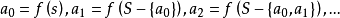
23。設S為一部分序集。 先把S整序化為ao, a1，””，ao,

(σ<τ)

然後令， 其中ρ為升鏈

B= {b_i：i<v}

的上界中(因一般說來，上界不只一個)所對應的a的

足指數中的最小序數且.如此下去，直到無法再作下去時， 即得S的一個極大元素。

3>4。設類F為在“⊂”關係下的一個部分序集(現在可叫部分序類).如果C是F中的集合排成的一個升鏈，則由有限特徵易知並集

A=∪{X：X∈C}

必屬於F，從而A就是C的一個上界。故F必有極大元素。

4>1。設F是由若干個非空集合作成的一個類。考慮

G={g：g為F的子類上的選擇函式}

把一個選擇函式看作一個集合時(即函式值作成的集合)，其子集合顯然即選擇函式。由此易知G具有限特徵， 故有極大元素f，於是f就必然是F上的一個選擇函式。證畢。

此定理中的命題是數學上經常要用到而且為大家所樂於使用的幾個主要而彼此等價的工具。除此以外，還有不少等價於它們的命題。