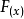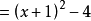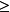相關詞條
- 單調區間
單調區間是指函式在某一區間內的函式值y,隨自變數x的值增大而增大(或減小)恆成立。若函式y=f(x)在某個區間是增函式或減函式,則就說函式在這一區間具有(嚴格...
- 單調性
函式的單調性(monotonicity)也可以叫做函式的增減性。當函式 f(x) 的自變數在其定義區間內增大(或減小)時,函式值f(x)也隨著增大(或減小),則稱該函式為在該...
- 單調函式
一般的,不強調區間的情況下,所謂的單調函式是指, 對於整個定義域而言,函式具有單調性。而不是針對定義域的子區間而言。舉個例子,反比例函式是一個具有單調性的...
- 單調遞增函式
高中數學教材定義(人民教育出版社,數學必修1,P28)一般地,設函式f(x)的定義域為I:如果對於定義域I內某個區間D上的任意兩個自變數的值x1,x2,當x1<x2時,都...
- 分段單調函式
分段單調函式是若干個單調函式相接的函式。分段單調函式的定義域可以分成有限個區間,在其中每一個區間上都是單調的一元函式。...
- 區間轉換法
區間轉換法是較常用的數學方法,它體現的是數學轉化與劃歸的數學思想方法。...... 顯然,π/5與17π/6不同在正弦函式的某個單調區間內。為了利用正弦函式單調性,...
- 單調佇列
單調佇列,即單調遞減或單調遞增的佇列。使用頻率不高,但在有些程式中會有非同尋常的作用。...
- 單調收斂定理
設0≤X1≤X2≤…≤Xn≤…是一單調非負隨機變數列。那么,若Xn(處處)收斂於隨機變數X,則相應的數學期望列EX1,EX2,…,EXn,…收斂於X的數學期望EX,這種現象稱...
- 增函式
設函式f(x)的定義域為D,如果對於定義域D內的某個區間上的任意兩個自變數的值x1, x2,當x1<x2時都有f(x1)<f(x2),那么就說f(x)在此區間上是增函式。...
- 減函式
函式f(x)的定義域為I,如果對於定義域I內的某個區間D上的任意兩個自變數的值x1,x2 ,當x1<x2時,都有f(x1)> f(x2),那么就說f(x)在這個區間上是減...
- 引理
求函式 的單調區間。 [3] 解:這是一個複合函式,設 ,由 ,解得 的定義域為 或 。先構造兩個引理:引理1:已知函式 ,若 在區間(a,b)上是增函式,其值域(...
- 對勾函式
研究推廣後的函式的單調性(只須寫出結論,不必證明),並求函式F(x) =(x^2+1/x)^n+(1/x^2+x)^n(n是正整數)在區間[1/2;,2]上的最大值和最小值(...
- 反正切函式
單調性 增函式 學科 數學目錄 1 定義 2 性質 3 計算 反正切函式定義 編輯 正切函式y=tanx在開區間(x∈(-π/2,π/2))的反函式,記作y=arctanx 或...
- 重排函式
重排函式(rearrangement function)是與可測函式等分布的單調函式。...... 一般的,不強調區間的情況下,所謂的單調函式是指, 對於整個定義域而言,函式具有單調性。而...
- 導數
可導函式的凹凸性與其導數的單調性有關。如果函式的導函式在某個區間上單調遞增,那么這個區間上函式是向下凹的,反之則是向上凸的。如果二階導函式存在,也可以用...
- 反三角函式
但是,在實函式中一般只研究單值函式,只把定義在包含銳角的單調區間上的基本三角函式的反函式,稱為反三角函式,這是亦稱反圓函式。為了得到單值對應的反三角函式,...