基本介紹
- 中文名:單調函式
- 外文名:Monotone function
- 定義:x1>x2,f(x1)≥(<=)f(x2)
- 學科:數學
- 特點:單調
- 判定方法:定義法、求導法
定義
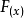
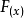
性質
基本性質
注意
- 函式的單調性也叫函式的增減性;
- 函式的單調性是對某個區間而言的,它是一個局部概念;
判定方法
定義法
- 設任意x1、x2∈給定區間,且x1<x2.
- 計算f(x1)- f(x2)至最簡。【最好表示為整式乘積的形式】
- 判斷上述差的符號。

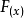
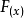
一般的,不強調區間的情況下,所謂的單調函式是指, 對於整個定義域而言,函式具有單調性。而不是針對定義域的子區間而言。舉個例子,反比例函式是一個具有單調性的...
增函式和減函式統稱為單調函式,嚴格增函式和嚴格減函式統稱為嚴格單調函式。...... 增函式和減函式統稱為單調函式,嚴格增函式和嚴格減函式統稱為嚴格單調函式。...
函式的單調性(monotonicity)也可以叫做函式的增減性。當函式 f(x) 的自變數在其定義區間內增大(或減小)時,函式值f(x)也隨著增大(或減小),則稱該函式為在該...
高中數學教材定義(人民教育出版社,數學必修1,P28)一般地,設函式f(x)的定義域為I:如果對於定義域I內某個區間D上的任意兩個自變數的值x1,x2,當x1<x2時,都...
分段單調函式是若干個單調函式相接的函式。分段單調函式的定義域可以分成有限個區間,在其中每一個區間上都是單調的一元函式。...
單調區間是指函式在某一區間內的函式值y,隨自變數x的值增大而增大(或減小)恆成立。若函式y=f(x)在某個區間是增函式或減函式,則就說函式在這一區間具有(嚴格...
在一點單調的函式(function monotone at apoint)當自變數逼近一點時,函式值單調變化的函式。...
單調數列指各項的值總是依次增加(或不減小)或總是依次減小(或不增加)的數列。...... 單調數列也就是定義在自然數集上的單調函式。上述定義與把單調函式的定義用...
重排函式(rearrangement function)是與可測函式等分布的單調函式。...... 重排函式(rearrangement function)是與可測函式等分布的單調函式。中文名 重排函式 外文名 ...
一般地,對數函式以冪(真數)為自變數,指數為因變數,底數為常量的函式。對數函式是6類基本初等函式之一。其中對數的定義:如果ax =N(a>0,且a≠1),那么數x叫做...
設0≤X1≤X2≤…≤Xn≤…是一單調非負隨機變數列。那么,若Xn(處處)收斂於隨機變數X,則相應的數學期望列EX1,EX2,…,EXn,…收斂於X的數學期望EX,這種現象稱...
單峰函式是在所考慮的區間中只有一個嚴格局部極大值(峰值)的實值函式。如果函式f(x)在區間[a, b]上只有唯一的最大值點C,而在最大值點C的左側,函式單調...
函式(function)表示每個輸入值對應唯一輸出值的一種對應關係。函式f中對應輸入值的輸出值x的標準符號為f(x)。包含某個函式所有的輸入值的集合被稱作這個函式的定義...
單調有界定理:若數列{an}遞增(遞減)有上界(下界),則數列{an}收斂,即單調有界數列必有極限。具體來說,如果一個數列單調遞增且有上界,或單調遞減且有下界,則該...
函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係可以用y...
在數學中,雙曲函式是一類與常見的三角函式(也叫圓函式)類似的函式。最基本的雙曲函式是雙曲正弦函式sinh和雙曲餘弦函式cosh,從它們可以導出雙曲正切函式tanh等,...
sinx函式,即正弦函式,三角函式的一種。正弦函式是三角函式的一種。對於任意一個實數x都對應著唯一的角(弧度制中等於這個實數),而這個角又對應著唯一確定的正弦值...
反正切函式(inverse tangent)是數學術語,反三角函式之一,指函式y=tanx的反函式。計算方法:設兩銳角分別為A,B,則有下列表示:若tanA=1.9/5,則 A=arctan1.9...
