基本介紹
定義
單調性
單調性的定義
單調性的證明
單調性的判斷方法
注意事項
性質
實例

 y=x^3的圖像
y=x^3的圖像
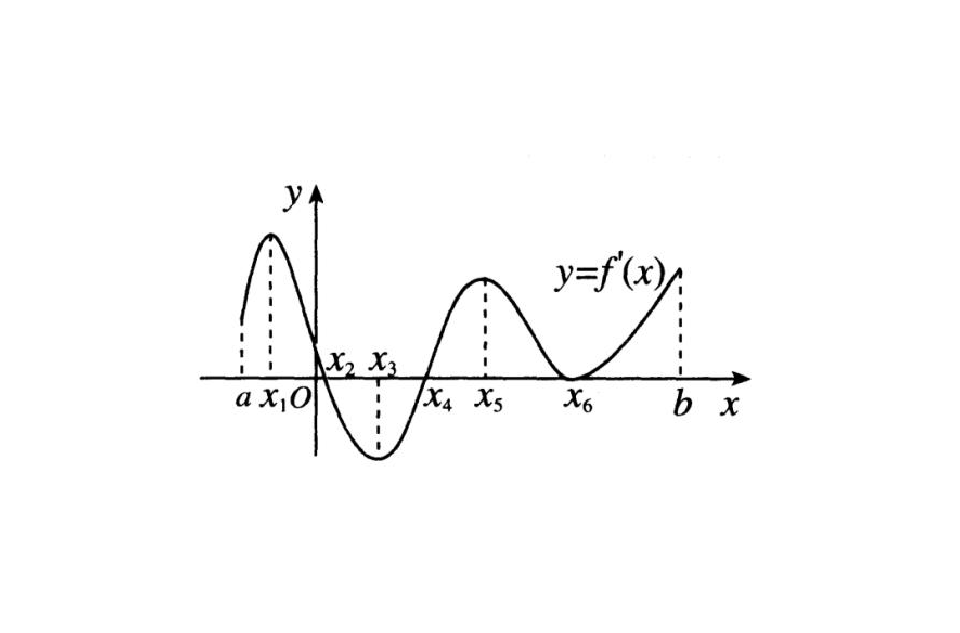

 y=x^3的圖像
y=x^3的圖像
函式f(x)的定義域為I,如果對於定義域I內的某個區間D上的任意兩個自變數的值x1,x2 ,當x1<x2時,都有f(x1)> f(x2),那么就說f(x)在這個區間上是減...
一般的,不強調區間的情況下,所謂的單調函式是指, 對於整個定義域而言,函式具有單調性。而不是針對定義域的子區間而言。舉個例子,反比例函式是一個具有單調性的...
增函式和減函式統稱為單調函式,嚴格增函式和嚴格減函式統稱為嚴格單調函式。...... 增函式和減函式統稱為單調函式,嚴格增函式和嚴格減函式統稱為嚴格單調函式。...
控制函式(dominating function)是一種特殊函式,是遞歸證明中常用的一種函式。若對某個a和任何x≥a,均有g(x)≤f(x),則稱f為g的控制函式(或稱f控制g,或f...
設f為定義在D上的函式, 若對任何x1、x2屬於D,當x1<x2時,總有f(x1)<=f(x2)則稱f為D上的增函式,若f(x1)<f(x2)則稱f為D上的嚴格增函式...
對勾函式是一種類似於反比例函式的一般雙曲函式,是形如f(x)=ax+b/x(a×b>0)的函式。由圖像得名,又被稱為“雙勾函式”、“勾函式”、"對號函式"、“...
上述理論完全可能推廣為如下形式:設ψ(x)是區間【α,b】上的非減函式,。如果定義在【α,b】上的函式ƒ(x)與g(x)滿足等式,則稱他們在[α,b]上關於權 ...
函式的單調性(monotonicity)也可以叫做函式的增減性。當函式 f(x) 的自變數在其定義區間內增大(或減小)時,函式值f(x)也隨著增大(或減小),則稱該函式為在該...
單調區間是指函式在某一區間內的函式值y,隨自變數x的值增大而增大(或減小)恆成立。若函式y=f(x)在某個區間是增函式或減函式,則就說函式在這一區間具有(嚴格...
引理2:已知函式 ,若 在區間(a,b)上是減函式,其值域為(c,d),又函式 在區間(c,d)上是增函式,那么,複合函式 在區間(c,d)上是減函式。...
餘切函式y=cotx x∈(0,π)的反函式叫做反餘切函式,記做y=arccotx。...... 反餘切函式y=arccotx在定義域R內是減函式。 反餘切函式y=arccotx即不是奇函式,...
