基本介紹
- 中文名:控制函式
- 外文名:dominating function
- 所屬領域:數理邏輯(遞歸論)
- 相關概念:遞歸證明、遞歸生成的函式集等
定義
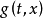
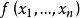
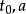

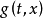
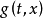
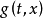
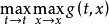
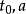
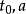
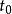
相關性質定理
定理1

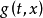
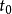
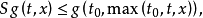
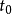

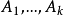
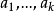
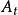
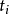

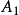
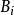


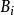








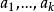
定義1


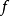
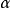



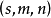
定義2

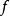
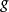
定理2
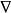

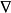
推論
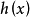
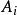
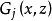

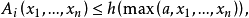

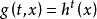

定義3
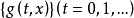
定義4
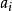
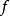
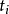
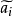

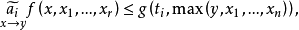
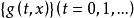
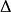
定理3

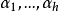
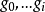
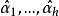


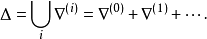
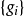

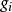
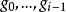
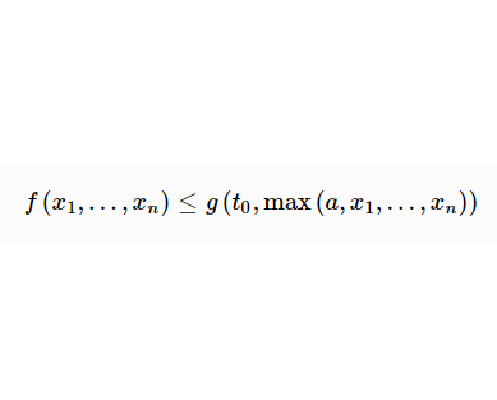
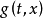
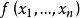
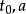

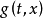
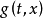
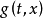
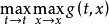
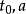
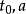
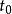

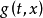
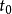
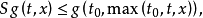
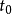

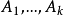
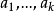
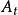
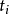

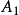
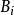


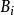








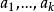


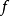
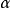



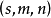

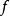
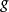
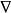

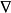
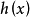
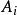
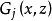

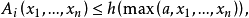

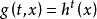

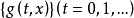
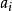
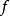
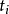
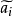

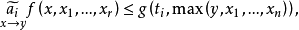
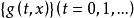
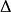

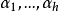
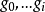
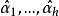


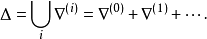
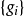

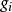
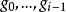
控制函式(dominating function)是一種特殊函式,是遞歸證明中常用的一種函式。若對某個a和任何x≥a,均有g(x)≤f(x),則稱f為g的控制函式(或稱f控制g,或f...
預測函式控制 (Predcitive Functoinal Contorl,簡稱PFC)是第三代模型預測控制算法,它是由 Richalet 和 Kuntze 等人在 80年代中後期提出,並成功地套用於工業機器...
傳遞函式是指零初始條件下線性系統回響(即輸出)量的拉普拉斯變換(或z變換)與激勵(即輸入)量的拉普拉斯變換之比。記作G(s)=Y(s)/U(s),其中Y(s)、U(s)...
在最佳控制模型(Optimal control model)中,考慮了操作員在作業中所採用的策略,即操作員根據不同的指令和不同的任務要求,表現出不同的作業方式。在最佳控制模型中,...
使用API函式CDdoor來控制光碟機門的開和關程式十分簡單,由於 CDdoor函式自身包含了對異常錯誤的處理機制,因此這個程式的通用性很高,你可以把這段代碼移植到你的程式中...
最優控制是指在給定的約束條件下,尋求一個控制,使給定的系統性能指標達到極大值(或極小值)。它反映了系統有序結構向更高水平發展的必然要求。它屬於最最佳化的...
滑模控制(sliding mode control, SMC)也叫變結構控制,本質上是一類特殊的非線性控制,且非線性表現為控制的不連續性。這種控制策略與其他控制的不同之處在於系統的...
控制形式是根據控制系統的參照量或控制量形成的特點對控制進行的分類。控制的目的不同,因而參照量的選擇和形成也就不同。一般可根據控制的目的,把參照量或控制量...
最優控制方法是對一個因果關係鏈偶合系統的運行過程施加控制以獲得最優的運行效果所使用的理論和方法體系。...
在數學分析和測度論中,勒貝格控制收斂定理提供了積分運算和極限運算可以交換運算順序的一個充分條件。在分析逐點收斂的函式數列的勒貝格積分時,積分號和逐點收斂的...
在工業過程控制中,按被控對象的實時數據採集的信息與給定值比較產生的誤差的比例、積分和微分進行控制的控制系統,簡稱PID控制系統。PID控制具有原理簡單,魯棒性強和...
控制參數(control parameter)影響系統狀態變數演化特徵的一些物理參數。與狀態變數比,這些參數變化緩慢,從而它們在系統數學模型中常可作為常數處理,以反映系統對環境的...
模型控制(Model control )是指一類預測控制算法,由內部模型、參考軌跡和控制算法三部分內容所組成。...
控制特性是指控制系統或儀器時所表現出的特性。研究正弦泵控液壓機蓄能器快鍛迴路控制特性的影響因素,不僅能為國內液壓機閥控液壓系提供理論指導,且有助統向泵控...
模式控制 解桐控制的一種1用於用狀態 方程描述的多變數控制系統間的解禍。當控制系統的狀態向 K}. .輸人控制向量和輸出控制向量二者的維數相同,且狀態方 程的...
系統傳遞函式(The system transfer function)是指零初始條件下線性系統回響(即輸出)量的拉普拉斯變換(或z變換)與激勵(即輸入)量的拉普拉斯變換之比。記作G(s)=Y...
相關函式是描述信號X(s),Y(t)(這兩個信號可以是隨機的,也可以是確定的)在任意兩個不同時刻s、t的取值之間的相關程度。...
參數控制,是指對變數系統實現的控制。指內在含量。例如:橡膠配方等。... 討論了疊代函式系IFS吸引子的參數控制,討論了IFS參數控制實現模擬樹木的方法。 [2] ...
函式(function)的定義通常分為傳統定義和近代定義,函式的兩個定義本質是相同的,只是敘述概念的出發點不同,傳統定義是從運動變化的觀點出發,而近代定義是從集合、...
控制策略是對某一系統或儀器進行控制的策略和方法。換電站主動控制策略由 2 部分組成,一為換電站在架空線路和電纜線路配電網中的故障判別與應對策略,二為配電網...
亨斯托克控制收斂定理是亨斯托克積分在積分號下取極限的定理。若{f n(x)}是[a,b]上的(H)可積函式列,且在[a,b]上幾乎處處收斂於f(x)。...
最優控制理論(optimal control theory),是現代控制理論的一個主要分支,著重於研究使控制系統的性能指標實現最最佳化的基本條件和綜合方法。 最優控制理論是研究和解決...
控制律( control law ),飛行控制系統形成控制指令的算法,描述了受控狀態變數與系統輸入信號之間的函式關係。...
有界控制(bounded control)值域屬於歐氏空間中的有界集合的控制函式.記r維歐氏空間R”中的集合U是系統的控制域.稱定義在時間區間「to ,t}]上的控制函式u(t)...
控制性能就是控制系統的性能,其評價分為動態性能指標和穩態性能指標兩類。系統的動態過程提供系統穩定性、回響速度及阻尼情況,表現為衰減、發散、等幅振盪等形式,由...
非線性控制理論常見非線性特性對系統運動的影響 從非線性環節的輸入與輸出之間存在的函式關係劃分,非線性特性可分為單值函式與多值函式兩類。例如死區特性、飽和特性...
自動控制理論是建立在頻率回響法和根軌跡法基礎上的一個分支。經典控制理論的研究對象是單輸入、單輸出的自動控制系統,特別是線性定常系統。經典控制理論的特點是以...
CallByName函式是一種語言參考,是指執行對象的方法,或者設定或返回對象的屬性的函式。...
閉環傳遞函式是廣泛套用在自動控制原理傳遞函式中的一個概念。... 閉環傳遞函式是廣泛套用在自動控制原理傳遞函式中的一個概念。中文名 閉環傳遞函式 套用 自動控制...
