模式控制
模式控制 解桐控制的一種1用於用狀態 方程描述的多變數控制系統間的解禍。當控制系統的狀態向 K}. .輸人控制向量和輸出控制向量二者的維數相同,且狀態方 程的係數矩陣A具有實數,相異的特徵值時則有A=E八 E‘,其中F.為右特徵向量,F一‘為左特徵向量‘八為特徵值 向量。可設計比例控制器K及模式補償器B}E,B一‘為狀 態方程係數矩陣的逆陣,並選擇輸出方程係數矩陣C一E一‘, 則可使其各控制器比例係數x,對各輸出變數的影響能相互 獨立。即實現各控制迴路相互不關聯的要求。
滑動模式控制
滑動模式控制(sliding mode)簡稱
SMC,是一種
非線性控制的技術,利用不連續的控制信號來調整
非線性系統的特性,強迫系統在二個系統的正常狀態之間滑動,最後進入穩態。其
狀態-
反饋控制律不是時間的
連續函式。相反的,控制律會依目前在狀態空間中的位置不同,可能從一個連續的控制系統切換到另一個連續的控制系統。因此滑動模型控制屬於
變結構控制。已針對滑動模型控制設計了許多的控制結構,目的是讓相空間圖中的軌跡可以前往和另一個控制結構之間相鄰的區域,因此最終的軌跡不會完全脫離某個控制結構。相反的,軌跡會在控制結構的邊界上“滑動”。這種沿著控制結構之間邊界滑動的行為稱為“滑動模式”而包括邊界在內的幾何軌跡稱為滑動曲面(sliding surface)。在現代控制理論的範圍中,任何
變結構系統(例如滑動模式控制)都可以視為是併合系統的特例,因為系統有些時候會在連續的狀態空間中移動,也時也會在幾個離散的控制模式中切換。
介紹
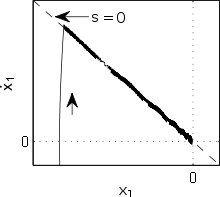
圖1:利用滑動模式控制器控制之系統的
相平面軌跡。在一開始的接觸階段後,系統沿著
的曲線滑行,
曲面是特別設計過的,系統在曲面上會有較理想的降階動態特性。此例中,
對應一階的
線性時不變系統,在原點處為指數穩定。
滑動模式控制中存在滑動曲面
,一開始時,系統會在有限時間內到達滑動曲面,之後就會沿著滑動曲面移動。在滑動模式的理論敘述中,系統會約束在滑動曲面上,因此只需將系統視為在滑動曲面上滑動。不過實際系統的實現是用高頻切換來讓系統近似在滑動曲面上滑動,高頻切換的控制信號讓系統在很鄰近滑動曲面的範圍內切跳(chatter),而且其頻率是不固定的。雖然整體系統是非線性的,不過圖1中,當系統到達滑動曲面後,理想(沒有切跳)系統會限制在
的滑動曲面上,滑動曲面是線性時不變系統,在原點處指數穩定。
直觀來說,滑動模式控制會配合很大的
增益(理想上可視為是無限大),強迫動態系統的軌跡無法離開滑動模式子空間太遠,必須沿著此子空間滑動。在降階滑動模式上的軌跡會有理想的動態特性(例如,系統會自然沿著此軌跡滑行,最後會停在理想的
駐點。滑動模式控制的主要優點是其強健性。因為控制很簡單,是在二個狀態之間(例如開/關或是正轉/反轉)切換,控制法則不需要精確,而且不會受到控制系統中參數的變異所影響。而且因為控制律不是
連續函式,滑動模式控制可以在有限時間內到達滑動曲面(比漸進到達的特性要好)在一些常見的條件下,
最優控制需要用到
起停式控制,而滑動模式控制中也有用到
起停式控制的特性,有些滑動模式控制也是某些控制系統下的最優控制。
有些交換式電源供應器驅動的電機就是利用滑動模式控制。這類轉換器本身就有不連續的特性,和不連續輸出的滑動模式控制器在本質上是一致的。使用連續性的控制器,還需要透過
脈衝寬度調變或是其他類似的技術來將連續性的輸出轉換為可用離散狀態表示的輸出。滑動模式控制在
機器人學有許多的套用。此控制算法特別已用在無人水面載具模擬在有大風大浪海面下的運作,其成功率相當高。
相較於其他有較多適度控制行為的
非線性控制,滑動模式控制因為其不連續的輸出,在套用上需要更謹慎的套用。特別是因為致動器本身的延遲以及其他實務上的限制,硬切換的滑動模式控制會產生顫動、能量損失、設備損壞,或是激發一些系統中的未建模動態。連續性的控制器設計比較不會有上述的問題,而且也可以設計一些接近滑動模式控制器的特性。
閉迴路解
此控制律不是
連續函式,也不會是
利普希茨連續,因此無法用
柯西-利普希茨定理確保閉迴路解的存在及唯一性。這個解需要用Filippov的架構來理解。。 大致上,沿著{\displaystyle \sigma (\mathbf {x} )=\mathbf {0} }的閉迴路系統可以用會平滑的動態{\displaystyle {\dot {\sigma }}(\mathbf {x} )=\mathbf {0} ;} 來近似,不過實際上不一定有這樣平滑的特性。高速的脈波振幅調變或ΔΣ調變產生的輸出是兩個狀態組成而成,但其有效的輸出會在連續的運動範圍內擺動。若是使用其他具有連續特性的
非線性控制設計可以避免這類的問題。有些情形下,滑動模式控制的設計可以用其他連續控制器來近似。