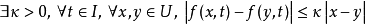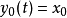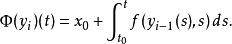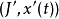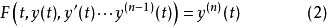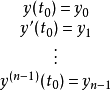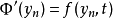柯西-利普希茨定理

在數學中，柯西-利普希茨定理（Cauchy-Lipschitz Theorem），又稱皮卡-林德勒夫定理（Picard-Lindelöf Theorem），保證了一元常微分方程的局部解以至最大解的存在性和唯一性。此定理最早由奧古斯丁·路易·柯西於1820年發表，但直到1868年，才由魯道夫·利普希茨給出確定的形式。另一個很常見的叫法是皮卡-林德勒夫定理，得名於數學家埃米爾·皮卡和恩斯特·林德勒夫。

基本介紹

• 中文名：柯西-利普希茨定理
• 外文名：Cauchy-Lipschitz Theorem
• 提出者：奧古斯丁·路易·柯西
• 提出時間：1820年
• 適用領域範圍：常微分方程
• 適用領域範圍：微積分

局部定理

設E為一個完備的有限維賦范向量空間（即一個巴拿赫空間），f為一個取值在E上的函式：

其中U為E中的一個開集，I是 中的一個區間。考慮以下的一階非線性微分方程：

如果f關於t連續，並在U中滿足利普希茨條件，也就是說，

那么對於任一給定的初始條件： ，其中 、 ，微分方程（1）存在一個解 (J,x(t))，其中 是一個包含 的區間，x(t) 是一個從 J 射到 U 的函式，滿足初始條件和微分方程。

局部唯一性：在包含點的足夠小的J區間上，微分方程（1）的解是唯一的（或者說，方程所有的解在足夠小的區間上都是重疊的）。

這個定理有點像物理學中的決定論思想：當我們知道了一個系統的特性（微分方程）和在某一時刻系統的情況（ ）時，下一刻的情況是唯一確定的。

驗證推導

一個簡潔的證明思路為構造一個總是滿足初始條件的函式遞歸序列 ，使得 ，這樣，如果這個序列有一個收斂點 y ，那么y為函式 的不動點，這時就有 ，於是我們構造出了一個解y。為此，我們從常數函式

開始。令

這樣構造出來的函式列中的每個函式都滿足初始條件。並且由於 f 在 U 中滿足利普希茨條件，當區間足夠小的時候， 成為一個收縮映射。根據完備空間的不動點存在定理，存在關於\Phi的穩定不動點，於是可知微分方程的解存在。

由於收縮映射的局部穩定不動點只有一個，因此在足夠小的區間內解是唯一的。

最大解定理

局部的柯西-利普希茨定理並沒有說明在較大區域上解的情況。事實上，對於微分方程（1）的任意解(J,x(t))、，定義一個序關係：(J,x(t))小於若且唯若 ，並且在J上的值與x(t)一樣。在這個定義之下，柯西-利普希茨定理斷言，微分方程的最大解是唯一存在的。

證明思路

解的唯一性：假設有兩個不同的最大解，那么由局部柯西-利普希茨定理可以證明其重疊部分的值相同，將兩者不同的部分分別延伸在重疊部分上，則會得到一個更“大”的解（只需驗證它滿足微分方程），矛盾。因此解唯一。

解的存在性：證明需要用到佐恩引理，構造所有解的並集。

定理推廣

擴展至高階常微分方程

對於一元的高階常微分方程

只需構造向量和相應的映射，就可以使得（2）變為。這時的初始條件為，即

擴展至偏微分方程

對於偏微分方程，有柯西-利普希茨定理的擴展形式：柯西-克瓦列夫斯基定理，保證了偏微分方程的解的存在性和唯一性。